A Cube Has 12 Of What
Juapaving
Apr 03, 2025 · 5 min read
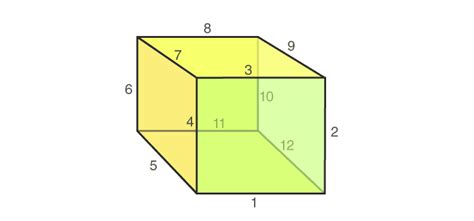
Table of Contents
A Cube Has 12 of What? Exploring the Geometry of Cubes
A cube, that fundamental three-dimensional shape, is a fascinating object of study in geometry. It's a simple yet powerful shape that forms the basis for many more complex structures. One of the most basic questions we can ask about a cube is: a cube has 12 of what? The answer, of course, is edges. But let's delve deeper than that simple answer, exploring the various geometric properties of a cube and how understanding these properties is crucial in various fields.
Understanding the Components of a Cube
Before we dive into the details of a cube's 12 edges, let's define the key components that make up this three-dimensional shape:
- Vertices: These are the corners of the cube, the points where three edges meet. A cube has 8 vertices.
- Edges: These are the line segments that connect two vertices. Crucially, a cube has 12 edges. These edges are all of equal length in a regular cube.
- Faces: These are the flat surfaces of the cube, each of which is a square. A cube has 6 faces.
These three components – vertices, edges, and faces – are fundamental to understanding the geometry of a cube and other polyhedra. The relationships between these elements are governed by Euler's formula, a fundamental theorem in topology: V - E + F = 2, where V represents the number of vertices, E represents the number of edges, and F represents the number of faces. For a cube, this formula holds true: 8 - 12 + 6 = 2.
The Significance of the 12 Edges
The 12 edges of a cube are more than just lines; they are the structural backbone of the shape. Their properties influence many aspects of the cube, including:
- Surface Area: The surface area of a cube is directly related to the length of its edges. If 'a' represents the length of one edge, the surface area is calculated as 6a². This formula highlights the critical role the edges play in determining the overall size of the cube's surface.
- Volume: The volume of a cube is also determined by the length of its edges. The volume is calculated as a³. This demonstrates the direct relationship between the edges and the three-dimensional space enclosed within the cube.
- Diagonal Length: The diagonal of a cube, which connects two opposite vertices, is another important measurement. It's related to the edge length by the formula √3a. Again, the edge length is fundamental in determining this critical diagonal dimension.
- Stability and Strength: In engineering and architecture, understanding the properties of a cube's edges is critical for ensuring structural stability. The arrangement and length of the edges impact the overall strength and resistance to stress and strain.
Cubes in Different Contexts: Beyond Geometry
The cube's 12 edges aren't just significant in pure geometry; their importance extends to various fields:
- Computer Graphics and Game Development: Cubes, and their derivatives, are fundamental building blocks in 3D modeling. Understanding the edges allows developers to precisely manipulate and render these shapes, creating realistic and immersive environments.
- Crystallography: Many crystalline structures have cubic forms, and the arrangement and properties of the edges are crucial for understanding their atomic structure and physical properties.
- Packaging and Logistics: Cubic shapes are highly efficient for packaging and shipping goods due to their stable structure and ability to maximize space. The edges dictate the dimensions of the packaging and its capacity.
- Art and Design: The cube's simple yet powerful form has been a recurring theme in art and design for centuries. Artists and designers utilize the cube's inherent geometry to create visually compelling and structurally sound works.
Exploring Different Types of Cubes
While we've primarily discussed regular cubes where all edges are of equal length, there are other types of cubes to consider:
- Skew Cubes: These cubes have edges that aren't necessarily perpendicular to each other, resulting in a distorted, non-regular cubic shape. While the number of edges remains 12, their lengths and angles vary.
- Hypercubes (Tesseracts): These are four-dimensional analogues of the cube. They possess far more complex properties, but they still retain some fundamental relationships to the three-dimensional cube. Understanding the properties of a three-dimensional cube's edges is a foundation for grasping the characteristics of higher-dimensional analogs.
Practical Applications: Calculating Properties of Cubes
Let's illustrate the practical application of understanding a cube's 12 edges with some example calculations:
Example 1: Calculating Surface Area and Volume
Imagine a cube with an edge length (a) of 5 centimeters.
- Surface Area: 6a² = 6 * (5 cm)² = 150 cm²
- Volume: a³ = (5 cm)³ = 125 cm³
Example 2: Calculating Diagonal Length
Using the same cube (a = 5 cm):
- Diagonal Length: √3a = √3 * 5 cm ≈ 8.66 cm
Beyond the Basics: Advanced Concepts
The seemingly simple cube holds many deeper mathematical and geometrical concepts:
- Symmetry: Cubes exhibit a high degree of symmetry, with multiple planes and axes of symmetry. Understanding these symmetries helps in various applications, from crystallography to art.
- Tessellations: Cubes can be used to create tessellations, which are repeating patterns that cover a plane without gaps or overlaps. This has applications in architecture and design.
- Topology: The study of topological properties of cubes relates to its connectedness and how it changes under continuous deformations.
Conclusion: The Ubiquitous Cube and its 12 Edges
The seemingly simple question "a cube has 12 of what?" leads us down a path exploring the fascinating geometry of cubes and their relevance across numerous disciplines. The 12 edges are not merely lines; they are the foundational elements that determine the cube's surface area, volume, diagonal length, stability, and overall characteristics. Understanding these properties is critical for anyone working in fields ranging from engineering and computer graphics to art and design. The cube, with its 12 edges, remains a cornerstone of geometry and a powerful symbol in many aspects of human endeavor. Its simplicity belies its depth and complexity, a testament to the elegance and power of fundamental geometric shapes. This exploration serves as a reminder that even the most basic shapes hold hidden depths waiting to be uncovered. The next time you encounter a cube, take a moment to appreciate its 12 edges and the rich geometry they represent.
Latest Posts
Latest Posts
-
Find The Prime Factorization Of 210
Apr 03, 2025
-
Biogeochemical Cycles Are Crucial To Ecosystem Function Because
Apr 03, 2025
-
Is Naoh A Base Or Acid
Apr 03, 2025
-
Is A Homogeneous Mixture A Solution
Apr 03, 2025
-
The Electrical Potential Energy Difference Between Two Points
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about A Cube Has 12 Of What . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
