The Electrical Potential Energy Difference Between Two Points.
Juapaving
Apr 03, 2025 · 6 min read
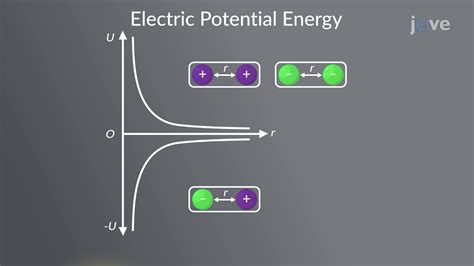
Table of Contents
The Electrical Potential Energy Difference Between Two Points: A Deep Dive
Understanding the electrical potential energy difference between two points is fundamental to grasping many key concepts in electricity and magnetism. This difference, often expressed as potential difference or voltage, drives the flow of charge and powers countless devices we use daily. This article delves into the intricacies of this crucial concept, exploring its definition, calculation, applications, and real-world implications.
What is Electrical Potential Energy?
Before we delve into the difference in electrical potential energy, let's establish a solid understanding of electrical potential energy itself. Imagine a positive charge placed near another positive charge. They repel each other, possessing a certain amount of stored energy due to their positions relative to one another – this is electrical potential energy. This energy is a consequence of the electrostatic force acting between charges. The closer the charges are, the higher the potential energy, and vice-versa. Conversely, a positive and negative charge attract each other; moving them further apart increases their electrical potential energy.
Think of it like a ball held at a certain height above the ground. The higher the ball, the greater its gravitational potential energy. Similarly, a charge positioned in a stronger electric field possesses higher electrical potential energy. This energy can be converted into other forms of energy, like kinetic energy, when the charge moves.
Factors Affecting Electrical Potential Energy
Several factors influence the electrical potential energy of a charge:
- Magnitude of the charge (q): A larger charge possesses greater potential energy in the same electric field.
- Strength of the electric field (E): A stronger electric field implies a greater force acting on the charge, leading to higher potential energy.
- Distance from the source charge: The distance between the charges significantly impacts the potential energy. The closer the charges, the greater the potential energy (for like charges).
- Electric field configuration: The arrangement of charges creating the electric field significantly influences the potential energy.
Understanding Potential Difference (Voltage)
The potential difference (ΔV), also known as voltage, is the difference in electrical potential energy per unit charge between two points in an electric field. It represents the work done per unit charge in moving a charge between those two points. In simpler terms, it's the "push" that drives the flow of electric charge.
ΔV = V<sub>B</sub> - V<sub>A</sub> = W<sub>AB</sub> / q
Where:
- ΔV represents the potential difference (voltage) between points A and B.
- V<sub>B</sub> is the electric potential at point B.
- V<sub>A</sub> is the electric potential at point A.
- W<sub>AB</sub> is the work done in moving a charge q from point A to point B.
- q is the magnitude of the charge.
The unit of potential difference is the volt (V), defined as one joule per coulomb (J/C). A potential difference of one volt means that one joule of work is done in moving one coulomb of charge between the two points.
Analogies to Understand Potential Difference
- Water Analogy: Imagine water flowing downhill. The height difference represents the potential difference. The greater the height difference, the faster the water flows. Similarly, a larger potential difference leads to a greater flow of charge (current).
- Gravitational Analogy: Consider a ball rolling down a hill. The difference in height corresponds to the potential difference. The steeper the hill, the faster the ball accelerates, much like a larger voltage drives a stronger current.
Calculating Potential Difference
Calculating the potential difference between two points depends on the specific electric field configuration. Here are some common scenarios:
1. Uniform Electric Field:
In a uniform electric field, the potential difference is simply the product of the electric field strength (E), the distance (d) between the points, and the cosine of the angle (θ) between the electric field and the displacement vector:
ΔV = -E * d * cos(θ)
The negative sign indicates that the potential decreases in the direction of the electric field.
2. Point Charge:
For a point charge (q), the electric potential (V) at a distance (r) from the charge is given by Coulomb's Law:
V = k * q / r
Where:
- k is Coulomb's constant (approximately 8.99 x 10<sup>9</sup> N⋅m<sup>2</sup>/C<sup>2</sup>).
To find the potential difference between two points at distances r<sub>A</sub> and r<sub>B</sub> from the point charge:
ΔV = V<sub>B</sub> - V<sub>A</sub> = k * q * (1/r<sub>B</sub> - 1/r<sub>A</sub>)
3. Multiple Charges:
For systems with multiple charges, the total potential at a point is the algebraic sum of the potentials due to each individual charge. The potential difference is then calculated by finding the difference in total potential between the two points. This requires careful consideration of the vector nature of electric fields and the principle of superposition.
Applications of Potential Difference
Potential difference is a fundamental concept with widespread applications in various fields, including:
- Electronics: Powering electronic circuits, from simple LEDs to complex microprocessors, relies heavily on precise control of potential differences. Batteries provide a potential difference, driving the flow of current through the circuit.
- Power Generation and Transmission: Power plants generate high potential differences to transmit electricity efficiently over long distances. Transformers are used to step up or step down the voltage for transmission and distribution.
- Medical Devices: Many medical instruments, such as electrocardiograms (ECGs) and electroencephalograms (EEGs), measure potential differences in the body to diagnose various conditions.
- Sensors: Numerous sensors rely on measuring potential differences to detect changes in physical or chemical properties. Examples include pressure sensors, temperature sensors, and pH sensors.
- Electrochemistry: Potential differences drive electrochemical reactions, crucial for applications like batteries, fuel cells, and electroplating.
Potential Difference and Electric Current
The potential difference between two points is directly related to the electric current flowing between those points. According to Ohm's Law:
V = I * R
Where:
- V is the potential difference (voltage).
- I is the electric current.
- R is the resistance.
This equation highlights the crucial relationship: a larger potential difference results in a greater current, provided the resistance remains constant. This relationship is fundamental to the design and operation of electrical circuits.
Measuring Potential Difference
Potential difference is measured using a voltmeter. A voltmeter is connected in parallel across the two points where the potential difference is to be measured. It has a high internal resistance to avoid significantly affecting the circuit's current.
Conclusion
The electrical potential energy difference between two points, or potential difference (voltage), is a cornerstone of electrical phenomena. Understanding this concept is critical for comprehending how electrical circuits work, how energy is transmitted, and how numerous devices operate. From powering our homes to enabling advanced medical technologies, potential difference plays a pivotal role in our modern world. By grasping the fundamental principles discussed in this article, one can gain a deeper appreciation for the complexities and wide-ranging applications of this fundamental concept in physics and engineering. Further exploration of topics like capacitance, electric fields, and circuit analysis will solidify this understanding and provide a broader perspective on the world of electricity.
Latest Posts
Latest Posts
-
4 Kingdoms Of The Domain Eukarya
Apr 04, 2025
-
A Bundle Of Muscle Fibers Is Called
Apr 04, 2025
-
A Force Is A Scalar Quantity True False
Apr 04, 2025
-
A Sound Wave Is An Example Of A Longitudinal Wave
Apr 04, 2025
-
Fundamental Building Block Of All Matter
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about The Electrical Potential Energy Difference Between Two Points. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
