Find The Prime Factorization Of 210
Juapaving
Apr 03, 2025 · 5 min read
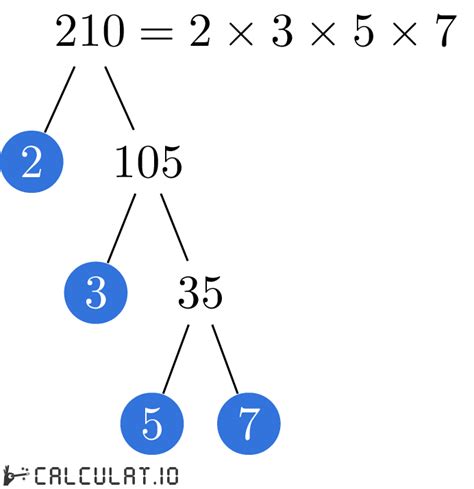
Table of Contents
Finding the Prime Factorization of 210: A Comprehensive Guide
Finding the prime factorization of a number is a fundamental concept in number theory. It involves breaking down a number into its prime components – numbers that are only divisible by 1 and themselves. This seemingly simple process has significant applications in various mathematical fields, from cryptography to simplifying complex calculations. This article delves into the method of finding the prime factorization of 210, explaining the process step-by-step and exploring related concepts. We'll also look at the broader implications of prime factorization and its usefulness in more advanced mathematical contexts.
Understanding Prime Numbers and Factorization
Before diving into the factorization of 210, let's establish a clear understanding of the core concepts.
What are Prime Numbers?
Prime numbers are whole numbers greater than 1 that are only divisible by 1 and themselves. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on. The number 1 is not considered a prime number. Prime numbers are the building blocks of all other whole numbers.
What is Prime Factorization?
Prime factorization (also known as prime decomposition) is the process of expressing a composite number (a number that is not prime) as a product of its prime factors. Every composite number can be uniquely expressed as a product of prime numbers, regardless of the order of the factors. This is known as the Fundamental Theorem of Arithmetic.
Finding the Prime Factorization of 210: A Step-by-Step Approach
Now, let's tackle the task at hand: finding the prime factorization of 210. We can use a simple method involving repeated division by prime numbers.
Step 1: Start with the smallest prime number, 2.
Is 210 divisible by 2? Yes, 210 / 2 = 105. Therefore, 2 is one of our prime factors.
Step 2: Continue with the next prime number, 3.
Is 105 divisible by 2? No. Let's move to the next prime number, 3. Is 105 divisible by 3? Yes, 105 / 3 = 35. So, 3 is another prime factor.
Step 3: Proceed with the next prime number, 5.
Is 35 divisible by 3? No. Is it divisible by the next prime number, 5? Yes, 35 / 5 = 7. Therefore, 5 is a prime factor.
Step 4: The final prime factor.
We are left with 7, which is itself a prime number.
Step 5: Combine the prime factors.
Therefore, the prime factorization of 210 is 2 x 3 x 5 x 7. We can write this as:
210 = 2 x 3 x 5 x 7
Alternative Methods for Prime Factorization
While the method above is straightforward, other techniques can be used, especially for larger numbers.
Factor Tree Method
The factor tree method is a visual approach to prime factorization. You start by branching out from the original number, representing its factors. You continue branching until you only have prime numbers at the ends of the branches. For 210:
210
/ \
2 105
/ \
3 35
/ \
5 7
The prime factors at the end of the branches are 2, 3, 5, and 7.
Division Method
The division method involves repeatedly dividing the number by its smallest prime factor until you reach 1. This is essentially the same as the step-by-step method described earlier.
Applications of Prime Factorization
Prime factorization, despite its seemingly simple nature, plays a crucial role in various mathematical applications:
Cryptography
Prime factorization is the foundation of many modern encryption methods, such as RSA encryption. The difficulty of factoring very large numbers into their prime components forms the basis of the security of these systems.
Number Theory
Prime factorization is a cornerstone of number theory, impacting concepts like modular arithmetic, Diophantine equations, and the study of prime number distribution. Understanding prime factorization allows mathematicians to analyze and solve problems involving divisibility, congruences, and other number-theoretic concepts.
Simplifying Fractions
In algebra and arithmetic, prime factorization helps simplify fractions to their lowest terms. By finding the prime factors of the numerator and denominator, you can identify common factors and cancel them out.
Finding the Greatest Common Divisor (GCD) and Least Common Multiple (LCM)
Prime factorization simplifies the calculation of the greatest common divisor (GCD) and least common multiple (LCM) of two or more numbers. The GCD is the largest number that divides all the given numbers without leaving a remainder, while the LCM is the smallest number that is a multiple of all the given numbers.
Exploring Prime Numbers Further
The study of prime numbers is an ongoing area of research in mathematics. Several intriguing questions and unsolved problems remain, such as:
-
The distribution of prime numbers: While there are patterns in the occurrence of prime numbers, predicting their distribution with absolute certainty is still an unsolved problem. The Prime Number Theorem gives an approximation but not a precise formula.
-
The twin prime conjecture: This conjecture states that there are infinitely many pairs of prime numbers that differ by 2 (e.g., 3 and 5, 11 and 13). While extensive computational evidence supports the conjecture, a rigorous mathematical proof remains elusive.
-
Goldbach's conjecture: This conjecture asserts that every even integer greater than 2 can be expressed as the sum of two prime numbers. This conjecture has been verified for incredibly large numbers, yet a definitive proof remains a significant challenge.
Conclusion: The Significance of Prime Factorization
Finding the prime factorization of 210 – a seemingly basic exercise – provides a stepping stone to understanding the profound implications of prime numbers in mathematics. From its crucial role in cryptography to its foundational place in number theory, prime factorization highlights the beauty and complexity inherent in the simplest of numbers. The continued exploration of prime numbers and their properties promises to unlock further insights into the structure and behavior of numbers themselves. The seemingly simple act of breaking down 210 into its prime factors opens the door to a vast and intriguing world of mathematical discovery. The exploration of prime numbers and their properties continues to captivate mathematicians and researchers, pushing the boundaries of our understanding of numbers and their intricate relationships.
Latest Posts
Latest Posts
-
Exterior Angle Of A Regular Hexagon
Apr 04, 2025
-
What Is The Radius Of Circle With Centre N
Apr 04, 2025
-
Pick Up The Incorrect Statement From The Following
Apr 04, 2025
-
Fe Iron Rusts Physical Or Chemical Change
Apr 04, 2025
-
The Eye And Ear Are Part Of
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Find The Prime Factorization Of 210 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
