Write The Prime Factorization Of 70
Juapaving
Mar 30, 2025 · 5 min read
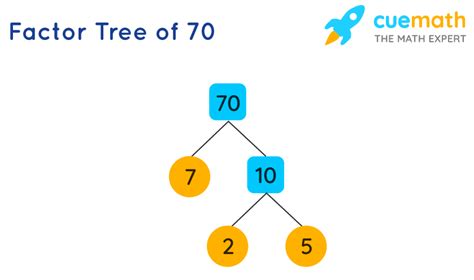
Table of Contents
Prime Factorization of 70: A Deep Dive into Number Theory
The seemingly simple question, "What is the prime factorization of 70?" opens a door to a fascinating world of number theory. While the answer itself is straightforward, exploring the process and the underlying concepts reveals fundamental principles crucial to understanding mathematics and computer science. This article will not only answer the question but delve deeply into the meaning and significance of prime factorization, exploring its applications and related mathematical ideas.
Understanding Prime Numbers
Before tackling the prime factorization of 70, let's solidify our understanding of prime numbers. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. In simpler terms, it's only divisible by 1 and itself. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on. The number 1 is not considered a prime number.
The fundamental theorem of arithmetic states that every integer greater than 1 can be represented uniquely as a product of prime numbers (ignoring the order of the factors). This theorem forms the foundation of prime factorization. This uniqueness is a key aspect; there's only one way to express a number as a product of primes.
Finding the Prime Factorization of 70
Now, let's find the prime factorization of 70. We can use a method called the factor tree. This involves repeatedly dividing the number by its smallest prime factor until we are left with only prime numbers.
-
Start with 70: The smallest prime number is 2, and 70 is an even number, so we can divide it by 2: 70 ÷ 2 = 35.
-
Divide 35: Now we have 35. 2 doesn't divide 35 evenly, but 5 does: 35 ÷ 5 = 7.
-
The Final Prime: 7 is a prime number. We've reached the end of our factor tree.
Therefore, the prime factorization of 70 is 2 x 5 x 7.
We can visually represent this with a factor tree:
70
/ \
2 35
/ \
5 7
Methods for Prime Factorization
While the factor tree method is intuitive and easy to visualize, especially for smaller numbers, other methods exist for finding the prime factorization of larger numbers. Let's explore a couple:
Repeated Division
This method systematically divides the number by increasingly larger prime numbers.
-
Start with the smallest prime (2): Check if the number is divisible by 2. If so, divide and repeat with the quotient.
-
Move to the next prime (3): If the number is not divisible by 2, check for divisibility by 3, and so on.
-
Continue until you reach a prime number: The process ends when the remaining number is itself a prime number.
Let's apply this to 70:
- 70 ÷ 2 = 35
- 35 ÷ 5 = 7
- 7 is prime
The prime factorization is 2 x 5 x 7.
Using Exponents
For numbers with repeated prime factors, it's often more concise to use exponents. For example, the prime factorization of 100 is 2 x 2 x 5 x 5, which can be written as 2² x 5². This notation is particularly useful for larger numbers.
Applications of Prime Factorization
Prime factorization may seem like a purely mathematical exercise, but it has numerous practical applications in various fields:
Cryptography
Prime factorization is fundamental to modern cryptography, especially in systems like RSA encryption. The security of RSA relies on the difficulty of factoring the product of two very large prime numbers. Finding the prime factors of a sufficiently large number is computationally extremely intensive, making it a secure basis for encryption.
Computer Science
Prime numbers and factorization play a crucial role in algorithms related to data structures and hashing. They are also used in generating pseudo-random numbers, essential for simulations and various computational tasks.
Number Theory
Prime factorization is central to many branches of number theory, including the study of modular arithmetic, Diophantine equations, and the distribution of prime numbers. Understanding prime factorization is essential for advanced mathematical research.
Beyond the Basics: Exploring Related Concepts
Understanding prime factorization leads to a broader appreciation of number theory concepts:
Greatest Common Divisor (GCD)
The greatest common divisor (GCD) of two or more numbers is the largest number that divides all of them without leaving a remainder. Prime factorization simplifies finding the GCD. By finding the prime factorization of each number, we can easily identify the common prime factors and their lowest powers to calculate the GCD.
For example, let's find the GCD of 70 and 105.
- Prime factorization of 70: 2 x 5 x 7
- Prime factorization of 105: 3 x 5 x 7
The common prime factors are 5 and 7. The lowest power of each is 5¹ and 7¹. Therefore, the GCD of 70 and 105 is 5 x 7 = 35.
Least Common Multiple (LCM)
The least common multiple (LCM) of two or more numbers is the smallest number that is a multiple of all of them. Prime factorization provides a straightforward method for finding the LCM. We identify all the prime factors present in the numbers and take the highest power of each.
Let's find the LCM of 70 and 105:
- Prime factorization of 70: 2 x 5 x 7
- Prime factorization of 105: 3 x 5 x 7
The prime factors are 2, 3, 5, and 7. The highest powers are 2¹, 3¹, 5¹, and 7¹. Therefore, the LCM of 70 and 105 is 2 x 3 x 5 x 7 = 210.
Distribution of Prime Numbers
The distribution of prime numbers along the number line is a fascinating and complex topic. The Prime Number Theorem provides an approximation of the number of primes less than a given number, illustrating the asymptotic behavior of prime numbers. The study of prime number distribution remains an active area of mathematical research.
Conclusion
The seemingly simple process of finding the prime factorization of 70 (2 x 5 x 7) serves as a gateway to a vast and intricate world of mathematical concepts. From its applications in cryptography and computer science to its fundamental role in number theory, prime factorization is a cornerstone of mathematical understanding. This exploration has highlighted not only the method of finding the prime factorization but also its significance and its connections to various related mathematical ideas, providing a deeper appreciation for the beauty and power of prime numbers. Further exploration into these fields promises to reveal even more fascinating aspects of this fundamental mathematical concept.
Latest Posts
Latest Posts
-
How Do You Write 19 In Roman Numerals
Apr 01, 2025
-
Why Is It Warmer When It Snows
Apr 01, 2025
-
A Positively Charged Ion Is Called
Apr 01, 2025
-
What Is This Phenomenon Known As
Apr 01, 2025
-
What Is The Ultimate Source Of Energy In Ecosystem
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Write The Prime Factorization Of 70 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
