Write The Prime Factorization Of 66
Juapaving
Mar 31, 2025 · 6 min read
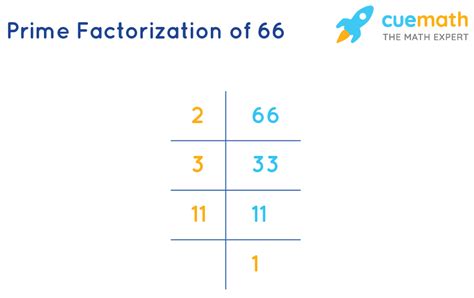
Table of Contents
Decomposing 66: A Deep Dive into Prime Factorization
Prime factorization. It sounds intimidating, doesn't it? Like some arcane mathematical ritual only performed by number theorists in dimly lit libraries. But in reality, prime factorization is a fundamental concept in mathematics, and understanding it opens doors to a deeper appreciation of numbers and their properties. Today, we'll explore this concept thoroughly, using the seemingly simple number 66 as our example. We'll break down 66 into its prime factors, and along the way, we'll explore related concepts like prime numbers, composite numbers, and the importance of prime factorization in various mathematical applications.
Understanding Prime and Composite Numbers
Before we delve into the prime factorization of 66, let's establish a solid foundation by defining key terms.
Prime Numbers: A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. In simpler terms, it's only divisible by 1 and itself. Examples include 2, 3, 5, 7, 11, and so on. 2 is the only even prime number; all other even numbers are divisible by 2.
Composite Numbers: A composite number is a positive integer that has at least one divisor other than 1 and itself. Essentially, it's a number that can be factored into smaller whole numbers. Examples include 4 (2 x 2), 6 (2 x 3), 9 (3 x 3), and so on.
1: The number 1 is neither prime nor composite. It's a special case.
Now that we've clarified these definitions, we can proceed to the main event: finding the prime factorization of 66.
Finding the Prime Factors of 66: A Step-by-Step Guide
The process of prime factorization involves repeatedly dividing a number by its smallest prime factor until you're left with only prime numbers. Let's apply this to 66:
-
Start with the smallest prime number: The smallest prime number is 2. Is 66 divisible by 2? Yes, 66 divided by 2 is 33.
-
Continue factoring: Now we have 2 x 33. Is 33 divisible by 2? No. Let's try the next prime number, 3. Is 33 divisible by 3? Yes, 33 divided by 3 is 11.
-
The final prime factor: Now we have 2 x 3 x 11. Both 2, 3, and 11 are prime numbers. We've reached the end of our factorization.
Therefore, the prime factorization of 66 is 2 x 3 x 11. This means that 66 can only be formed by multiplying these three prime numbers together. No other combination of prime numbers will yield 66.
The Uniqueness of Prime Factorization: The Fundamental Theorem of Arithmetic
The fact that we arrived at a unique prime factorization for 66 isn't a coincidence. This is guaranteed by the Fundamental Theorem of Arithmetic, which states that every integer greater than 1 can be represented uniquely as a product of prime numbers (disregarding the order of the factors). This theorem is a cornerstone of number theory and has profound implications in various branches of mathematics.
Applications of Prime Factorization
Prime factorization might seem like a purely theoretical exercise, but it has practical applications in various fields:
1. Cryptography: Securing Online Transactions
Prime factorization plays a crucial role in modern cryptography, particularly in public-key cryptography systems like RSA. These systems rely on the difficulty of factoring extremely large numbers into their prime factors. The vast computational power required to factor these huge numbers ensures the security of online transactions and sensitive data.
2. Simplifying Fractions: Finding the Greatest Common Divisor (GCD)
Prime factorization is a powerful tool for simplifying fractions. By finding the prime factors of the numerator and denominator, we can easily identify the greatest common divisor (GCD). The GCD allows us to reduce the fraction to its simplest form. For example, consider the fraction 66/90. The prime factorization of 66 is 2 x 3 x 11, and the prime factorization of 90 is 2 x 3 x 3 x 5. The GCD is 2 x 3 = 6. Therefore, 66/90 simplifies to 11/15.
3. Finding the Least Common Multiple (LCM): Solving Problems Involving Rhythms and Cycles
Prime factorization is also useful for determining the least common multiple (LCM) of two or more numbers. The LCM is the smallest number that is a multiple of all the given numbers. This has applications in various areas, including scheduling tasks with repeating cycles (e.g., determining when two machines operating at different intervals will coincide) or in music theory when finding the least common denominator for rhythmic patterns.
4. Abstract Algebra: Building Mathematical Structures
Prime factorization is a building block in abstract algebra, a branch of mathematics concerned with algebraic structures such as groups, rings, and fields. The properties of prime numbers and their factorizations provide insights into the structure and behavior of these algebraic objects.
Beyond 66: Exploring Other Factorizations
While we've focused on 66, the principles discussed apply to any composite number. Let's briefly explore the prime factorization of some related numbers:
- 65: 5 x 13
- 67: This is a prime number itself; its only factors are 1 and 67.
- 68: 2 x 2 x 17 (or 2² x 17)
- 69: 3 x 23
- 70: 2 x 5 x 7
Notice the patterns and the variations in the number and types of prime factors that arise.
Practical Tips for Prime Factorization
While there's no magic formula, here are some tips for efficiently determining prime factorizations:
- Start with the smallest prime factors: Begin by dividing by 2, then 3, then 5, and so on. This systematic approach ensures you don't miss any prime factors.
- Use a factor tree: A factor tree is a visual representation of the factorization process. It can be particularly helpful for larger numbers.
- Utilize online calculators (for large numbers): For extremely large numbers, online calculators can be incredibly useful. However, understanding the underlying process remains crucial.
Conclusion: The Power of Prime Factorization
Prime factorization, although seemingly simple on the surface, is a powerful concept with far-reaching implications in mathematics and beyond. By understanding how to decompose numbers into their prime components, we unlock insights into their properties and utilize this knowledge in various fields, from securing online transactions to simplifying complex mathematical problems. While we used 66 as our example, the principles and techniques learned can be applied to any composite number, enriching our understanding of the fundamental building blocks of numbers. The journey of exploring prime factorization is an ongoing one, revealing the elegance and power inherent within the seemingly simple world of numbers.
Latest Posts
Latest Posts
-
Find The Mean Proportional Between 3 And 27
Apr 02, 2025
-
What Shape Has 12 Edges 8 Vertices And 6 Faces
Apr 02, 2025
-
Different Ways To Write A Number
Apr 02, 2025
-
Least Common Multiple Of 8 And 4
Apr 02, 2025
-
How Many Neutrons Are In Potassium
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Write The Prime Factorization Of 66 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
