If Diagonals Of A Quadrilateral Bisect Each Other
Juapaving
Apr 02, 2025 · 6 min read
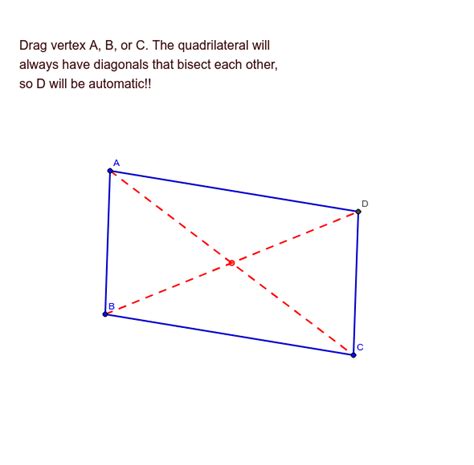
Table of Contents
If the Diagonals of a Quadrilateral Bisect Each Other
The properties of quadrilaterals, those four-sided polygons that form the building blocks of many geometric shapes and structures, are a fascinating area of study. One particularly intriguing property involves the diagonals of a quadrilateral – the line segments connecting opposite vertices. Specifically, we'll explore the question: If the diagonals of a quadrilateral bisect each other, what can we conclude about the quadrilateral?
Understanding the Problem
Before diving into the solution, let's establish a clear understanding of the terms involved. A quadrilateral is simply a polygon with four sides. The diagonals of a quadrilateral are line segments connecting non-adjacent vertices. When we say the diagonals bisect each other, we mean that each diagonal is divided into two equal parts by the intersection point. In other words, the point of intersection is the midpoint of each diagonal.
This isn't true for all quadrilaterals. Consider a rectangle: its diagonals bisect each other. Now consider a parallelogram: its diagonals also bisect each other. However, a trapezoid, generally speaking, does not possess this property.
The Key Theorem: Parallelograms
The crucial theorem that connects bisecting diagonals to a specific type of quadrilateral is this: If the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram.
This is a fundamental theorem in geometry, and its proof relies on establishing the congruence of triangles formed by the intersecting diagonals. Let's delve into the proof:
Proof: Diagonals Bisecting Each Other Implies Parallelogram
Let's consider a quadrilateral ABCD, where the diagonals AC and BD intersect at point O. We are given that the diagonals bisect each other, meaning AO = OC and BO = OD. We want to prove that ABCD is a parallelogram.
1. Congruent Triangles:
Consider triangles ΔAOB and ΔCOD. We have:
- AO = OC (Given)
- BO = OD (Given)
- ∠AOB = ∠COD (Vertically opposite angles are equal)
By the Side-Angle-Side (SAS) congruence criterion, ΔAOB ≅ ΔCOD. This congruence implies that AB = CD (corresponding sides of congruent triangles are equal).
2. More Congruent Triangles:
Now, let's consider triangles ΔBOC and ΔDOA. We have:
- BO = OD (Given)
- OC = OA (Given)
- ∠BOC = ∠DOA (Vertically opposite angles are equal)
Again, by the SAS congruence criterion, ΔBOC ≅ ΔDOA. This congruence implies that BC = DA (corresponding sides of congruent triangles are equal).
3. Opposite Sides are Equal:
From steps 1 and 2, we've established that AB = CD and BC = DA. This means that the opposite sides of quadrilateral ABCD are equal in length.
4. Parallelogram Conclusion:
A quadrilateral with opposite sides equal in length is a parallelogram. Therefore, ABCD is a parallelogram.
This completes the proof. The fact that the diagonals bisect each other is a sufficient condition to conclude that the quadrilateral is a parallelogram.
Converse of the Theorem
It's important to note the converse of this theorem is also true: If a quadrilateral is a parallelogram, then its diagonals bisect each other. This can be proven using similar triangle congruence arguments. The equality of opposite sides in a parallelogram leads to the congruence of triangles formed by the diagonals, ultimately demonstrating that the diagonals bisect each other.
Applications and Significance
Understanding this property of parallelograms has significant applications in various areas:
-
Engineering and Construction: Parallelograms and their properties are essential in structural design and construction. The stability and strength of many structures rely on the principles of parallelogram geometry.
-
Computer Graphics: In computer graphics and animation, transformations and manipulations of shapes often involve parallelograms and their properties. Understanding how diagonals bisect in a parallelogram is crucial for accurate geometric calculations.
-
Physics: Many physical phenomena, such as forces and vectors, can be represented and analyzed using parallelogram models. The bisecting diagonals property simplifies calculations and analysis.
-
Mathematics: This theorem is a fundamental building block for more advanced geometric concepts and proofs. It forms the foundation for understanding other quadrilateral properties and relationships.
Beyond Parallelograms: Special Cases
While the theorem states that bisecting diagonals imply a parallelogram, it's important to consider special cases of parallelograms:
-
Rectangles: Rectangles are parallelograms with right angles. Their diagonals not only bisect each other but are also equal in length.
-
Rhombuses: Rhombuses are parallelograms with all sides equal in length. Their diagonals bisect each other and are perpendicular.
-
Squares: Squares are both rectangles and rhombuses. Their diagonals bisect each other, are equal in length, and are perpendicular.
These special cases demonstrate that the property of bisecting diagonals is a necessary but not sufficient condition for a quadrilateral to be a square, rectangle or rhombus.
Problem Solving: Illustrative Examples
Let's illustrate the application of this theorem with some examples:
Example 1:
Given a quadrilateral with vertices A(1, 2), B(3, 4), C(5, 2), and D(3, 0). Determine if the diagonals bisect each other.
Solution:
Find the midpoint of AC: ((1+5)/2, (2+2)/2) = (3, 2)
Find the midpoint of BD: ((3+3)/2, (4+0)/2) = (3, 2)
Since the midpoints are the same, the diagonals bisect each other. Therefore, the quadrilateral ABCD is a parallelogram.
Example 2:
A quadrilateral has diagonals that bisect each other at right angles. What type of quadrilateral is it?
Solution:
Since the diagonals bisect each other, the quadrilateral is a parallelogram. Because the diagonals bisect at right angles, it is a rhombus. Note: it could also be a square, which is a special case of a rhombus.
Example 3:
Prove that if the diagonals of a quadrilateral are equal in length and bisect each other, the quadrilateral is a rectangle.
Solution:
Since the diagonals bisect each other, the quadrilateral is a parallelogram. We are given that the diagonals are equal in length. In a parallelogram, equal diagonals imply a rectangle. Therefore, the quadrilateral is a rectangle.
These examples demonstrate how the knowledge of bisecting diagonals allows us to deduce valuable information about the properties and type of the quadrilateral.
Conclusion: A Fundamental Geometric Property
The property that the diagonals of a quadrilateral bisect each other is a fundamental concept in geometry. Its connection to parallelograms provides a powerful tool for analyzing and classifying quadrilaterals. Understanding this theorem, its proof, and its implications is crucial for anyone studying geometry, from high school students to advanced mathematicians and engineers. This knowledge lays the groundwork for exploring more complex geometric relationships and applications. The ability to identify parallelograms based on their bisecting diagonals simplifies geometric problem-solving and offers a deeper appreciation for the elegance and structure of geometry. Remember, the converse is also true, solidifying the strong link between bisecting diagonals and the parallelogram family of quadrilaterals.
Latest Posts
Latest Posts
-
Choose The True Statement About The Krebs Cycle
Apr 03, 2025
-
Essay On The Pleasure Of Reading
Apr 03, 2025
-
Compare And Contrast Pulmonary Circulation With Systemic Circulation
Apr 03, 2025
-
Does Photosynthesis Take Place Primarily In Plant Leaves
Apr 03, 2025
-
A Sphere Is Inscribed In A Cube
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about If Diagonals Of A Quadrilateral Bisect Each Other . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
