Write 84 As A Product Of Prime Factors
Juapaving
Mar 24, 2025 · 5 min read
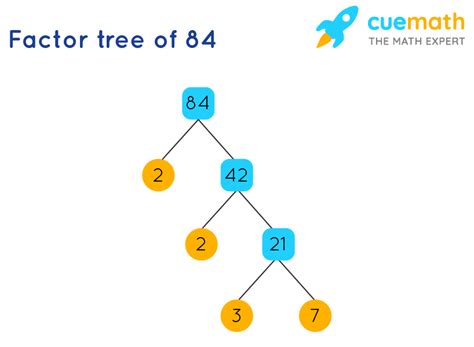
Table of Contents
Writing 84 as a Product of Prime Factors: A Comprehensive Guide
Finding the prime factorization of a number is a fundamental concept in number theory. It's the process of expressing a composite number as a product of its prime factors. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. This article will thoroughly explore how to write 84 as a product of its prime factors, covering multiple methods and expanding upon the underlying mathematical principles. We'll also delve into the broader significance of prime factorization in mathematics and its practical applications.
Understanding Prime Factorization
Before diving into the specific case of 84, let's solidify our understanding of prime factorization. The fundamental theorem of arithmetic states that every integer greater than 1 can be uniquely represented as a product of prime numbers (ignoring the order of the factors). This unique representation is crucial in various mathematical operations and provides a foundation for many advanced concepts.
Why is Prime Factorization Important?
Prime factorization is not just an academic exercise. It's a cornerstone of many mathematical concepts, including:
- Greatest Common Divisor (GCD): Finding the GCD of two or more numbers is simplified by first finding their prime factorizations. The GCD is the product of the common prime factors raised to the lowest power.
- Least Common Multiple (LCM): Similarly, finding the LCM is streamlined using prime factorization. The LCM is the product of all prime factors raised to the highest power present in any of the numbers.
- Simplifying Fractions: Prime factorization helps in simplifying fractions to their lowest terms by canceling out common factors in the numerator and the denominator.
- Cryptography: Prime numbers and their properties are fundamental to modern cryptography, playing a critical role in securing online transactions and data.
Methods for Finding the Prime Factorization of 84
There are several approaches to determine the prime factorization of 84. Let's explore the most common methods:
Method 1: Factor Tree
A factor tree is a visual method that systematically breaks down a number into its prime factors.
-
Start with the number 84: Write 84 at the top of your factor tree.
-
Find a pair of factors: Find two numbers that multiply to 84. For example, 2 and 42. Branch out from 84 to 2 and 42.
-
Continue factoring: Now, look at 42. It can be factored into 2 and 21. Branch out from 42 to 2 and 21.
-
Prime factors: 2 is a prime number. 21 can be factored into 3 and 7, both of which are prime numbers. Branch out from 21 to 3 and 7.
-
The prime factorization: Once all branches end in prime numbers, you have the prime factorization. In this case, the prime factors of 84 are 2, 2, 3, and 7.
Therefore, the prime factorization of 84 is 2 x 2 x 3 x 7, which can also be written as 2² x 3 x 7.
Method 2: Division by Prime Numbers
This method involves repeatedly dividing the number by the smallest prime number that divides it evenly until you reach 1.
-
Start with 84: Divide 84 by the smallest prime number, 2. 84 / 2 = 42.
-
Divide the result: Divide 42 by 2. 42 / 2 = 21.
-
Continue dividing: 21 is not divisible by 2, but it is divisible by 3. 21 / 3 = 7.
-
Prime factor reached: 7 is a prime number. The process ends here.
-
The prime factorization: The prime factors are the divisors used in each step: 2, 2, 3, and 7.
This confirms the prime factorization of 84 as 2² x 3 x 7.
Method 3: Systematic Division
This method is a more organized version of the division method. It systematically checks for divisibility by prime numbers in ascending order.
| Number | Divisor | Quotient |
|---|---|---|
| 84 | 2 | 42 |
| 42 | 2 | 21 |
| 21 | 3 | 7 |
| 7 | 7 | 1 |
The divisors are 2, 2, 3, and 7. Therefore, the prime factorization is 2² x 3 x 7.
Applying Prime Factorization: Examples
Let's illustrate the practical application of prime factorization with some examples:
Example 1: Finding the GCD of 84 and 120
- Prime factorization of 84: 2² x 3 x 7
- Prime factorization of 120: 2³ x 3 x 5
The common prime factors are 2 and 3. The lowest power of 2 is 2¹, and the lowest power of 3 is 3¹. Therefore, the GCD(84, 120) = 2 x 3 = 6.
Example 2: Finding the LCM of 84 and 120
- Prime factorization of 84: 2² x 3 x 7
- Prime factorization of 120: 2³ x 3 x 5
The prime factors involved are 2, 3, 5, and 7. The highest power of 2 is 2³, the highest power of 3 is 3¹, the highest power of 5 is 5¹, and the highest power of 7 is 7¹. Therefore, the LCM(84, 120) = 2³ x 3 x 5 x 7 = 840.
Example 3: Simplifying Fractions
Consider the fraction 84/120. Using the prime factorizations from the previous examples:
84/120 = (2² x 3 x 7) / (2³ x 3 x 5)
Canceling out common factors (2² and 3):
84/120 = 7 / (2 x 5) = 7/10
This demonstrates how prime factorization simplifies fraction reduction.
Conclusion: The Power of Prime Factorization
Writing 84 as a product of its prime factors (2² x 3 x 7) is more than just a mathematical exercise. It's a fundamental skill that unlocks a deeper understanding of number theory and its applications. From finding GCDs and LCMs to simplifying fractions and contributing to the foundations of cryptography, the ability to prime factorize numbers is an essential tool in various mathematical contexts. Mastering this skill strengthens your mathematical foundation and opens doors to more advanced concepts. By understanding the different methods outlined above—factor trees, division by prime numbers, and systematic division—you can confidently tackle prime factorization problems of varying complexities. Remember, practice is key to building proficiency in this crucial mathematical skill.
Latest Posts
Latest Posts
-
How Many Valence Electrons Are In Oxygen
Mar 28, 2025
-
Which Of The Following Letters Does Not Suffer Lateral Inversion
Mar 28, 2025
-
Is 53 A Prime Number Or A Composite Number
Mar 28, 2025
-
What Is The Least Common Multiple Of 24 And 15
Mar 28, 2025
-
What Percent Is 2 3 Of A Circle
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about Write 84 As A Product Of Prime Factors . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
