What Percent Is 2 3 Of A Circle
Juapaving
Mar 29, 2025 · 5 min read
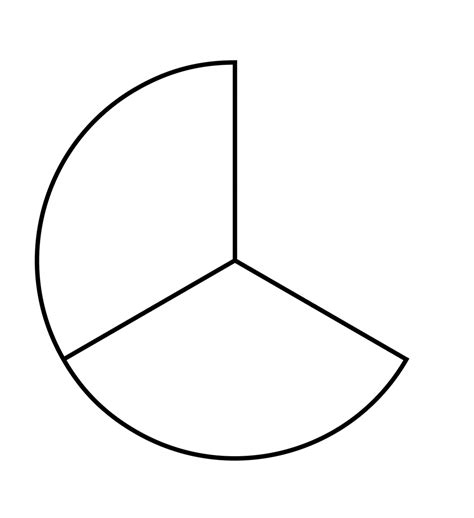
Table of Contents
What Percent is 2/3 of a Circle? Understanding Fractions and Percentages in Geometry
Circles, those perfectly symmetrical shapes, often feature in mathematical problems involving fractions and percentages. A common question, and the focus of this article, is: what percentage represents two-thirds (2/3) of a circle? This seemingly simple question opens the door to understanding fundamental concepts in mathematics, particularly the relationship between fractions, decimals, and percentages. We'll delve into the calculation, explore related concepts, and provide practical examples to solidify your understanding.
Understanding the Basics: Fractions, Decimals, and Percentages
Before tackling the core question, let's refresh our understanding of the three key mathematical concepts involved:
Fractions: Representing Parts of a Whole
Fractions represent parts of a whole. They are expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered. In our case, 2/3 signifies that a whole is divided into three equal parts, and we're interested in two of those parts.
Decimals: Expressing Fractions in Base 10
Decimals are another way of representing fractions. They use the base-10 number system, where each place value to the right of the decimal point represents a power of 10 (tenths, hundredths, thousandths, and so on). Converting a fraction to a decimal involves dividing the numerator by the denominator.
Percentages: Expressing Fractions as Parts of 100
Percentages express fractions as parts of 100. The symbol "%" represents "per hundred," indicating the number of parts out of 100. Converting a fraction or decimal to a percentage involves multiplying by 100 and adding the "%" symbol.
Calculating the Percentage: 2/3 of a Circle
Now, let's address the central question: what percent is 2/3 of a circle? The approach is straightforward:
-
Convert the fraction to a decimal: Divide the numerator (2) by the denominator (3): 2 ÷ 3 ≈ 0.6667 (we'll use a rounded value for simplicity).
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add the "%" symbol: 0.6667 x 100 ≈ 66.67%.
Therefore, 2/3 of a circle represents approximately 66.67% of the circle.
Precision and Recurring Decimals
It's important to note that the decimal representation of 2/3 (0.666...) is a recurring decimal – the digit 6 repeats infinitely. Our calculation used a rounded value for practicality. For highly precise calculations, you might use the exact fraction 2/3 or a more extended decimal representation.
Practical Applications and Related Concepts
The concept of finding percentages of a circle has practical applications in various fields:
Data Visualization: Pie Charts
Pie charts are a common data visualization tool that uses circular sectors to represent proportions of a whole. Understanding how to calculate percentages of a circle is crucial for accurately creating and interpreting pie charts. If a pie chart represents total sales, and a sector represents sales of a particular product accounting for 2/3 of the total, you now know it accounts for 66.67% of the total sales.
Geometry and Trigonometry: Sectors and Arcs
In geometry, a sector is a part of a circle enclosed by two radii and an arc. Calculating the area or arc length of a sector often involves working with fractions and percentages of a circle. Understanding the relationship between the fraction representing the sector and its percentage helps to perform calculations related to area and circumference.
Circular Motion and Angular Displacement
In physics, understanding fractions and percentages of a circle is vital when dealing with circular motion. Angular displacement, the change in an object's angle during rotation, can be expressed as a fraction or percentage of a full circle (360 degrees). For example, an angular displacement of 240 degrees would be (240/360) = (2/3) or 66.67% of a full revolution.
Further Exploration: Working with Other Fractions of a Circle
Let's extend our understanding by exploring how to calculate the percentage for other fractions of a circle:
1/4 of a Circle:
- Convert the fraction to a decimal: 1 ÷ 4 = 0.25
- Convert the decimal to a percentage: 0.25 x 100 = 25%
Therefore, 1/4 of a circle is 25%.
1/2 of a Circle:
- Convert the fraction to a decimal: 1 ÷ 2 = 0.5
- Convert the decimal to a percentage: 0.5 x 100 = 50%
Therefore, 1/2 of a circle is 50%.
3/4 of a Circle:
- Convert the fraction to a decimal: 3 ÷ 4 = 0.75
- Convert the decimal to a percentage: 0.75 x 100 = 75%
Therefore, 3/4 of a circle is 75%.
Working with More Complex Fractions:
The same principles apply to more complex fractions. For instance, to find the percentage for 5/8 of a circle:
- Convert the fraction to a decimal: 5 ÷ 8 = 0.625
- Convert the decimal to a percentage: 0.625 x 100 = 62.5%
Therefore, 5/8 of a circle is 62.5%.
Conclusion: Mastering Fractions, Decimals, and Percentages in Circular Calculations
Understanding the relationship between fractions, decimals, and percentages is crucial for solving various mathematical problems involving circles. The calculation of what percentage represents two-thirds of a circle is a fundamental example showcasing this relationship. By mastering these concepts, you'll be better equipped to tackle more complex geometrical and mathematical challenges across numerous fields, from data analysis to engineering. Remember the simple steps of converting fractions to decimals and then to percentages, and you'll be able to confidently calculate the percentage representation of any fractional part of a circle. This knowledge provides a strong foundation for further exploration of geometry, trigonometry, and other related fields.
Latest Posts
Latest Posts
-
What Is The Least Common Denominator Of 8 And 12
Mar 31, 2025
-
5 Letter Words With Er In The End
Mar 31, 2025
-
What Are The Common Factors Of 28 And 36
Mar 31, 2025
-
What Is 6 10 As A Percentage
Mar 31, 2025
-
Cual Es La Diferencia Entre Sent Y Send
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 2 3 Of A Circle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
