Which Set Of Angles Can Form A Triangle
Juapaving
Apr 05, 2025 · 5 min read
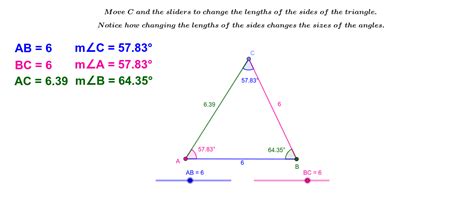
Table of Contents
Which Sets of Angles Can Form a Triangle? A Comprehensive Guide
Understanding which sets of angles can form a triangle is fundamental to geometry. It's a concept that builds the foundation for more complex geometrical theorems and problem-solving. This comprehensive guide will explore the rules governing triangle angle formation, delve into different types of triangles based on their angles, and offer practical examples to solidify your understanding.
The Triangle Angle Sum Theorem: The Cornerstone
The most crucial rule governing triangle angles is the Triangle Angle Sum Theorem. This theorem states that the sum of the interior angles of any triangle always equals 180 degrees. This is true regardless of the triangle's size, shape, or type. This seemingly simple theorem is the bedrock upon which all other angle-related properties of triangles are built.
Understanding Interior Angles
Before we delve deeper, let's clarify what "interior angles" mean. Interior angles are the angles inside the triangle, formed by the intersection of two sides. They are the angles we're concerned with when determining if a set of angles can create a triangle.
Sets of Angles that Can Form a Triangle: The Rules
To determine if a given set of angles can form a triangle, you simply need to add them together. If their sum is exactly 180 degrees, then they can form a triangle. If the sum is less than 180 degrees, they cannot. If the sum exceeds 180 degrees, they cannot either.
Here's a breakdown:
- Sum = 180 degrees: The angles can form a triangle.
- Sum < 180 degrees: The angles cannot form a triangle. The resulting shape would be a concave polygon. Imagine trying to create a triangle with angles of 30°, 40°, and 50°; the sum is 120°, leaving a significant gap.
- Sum > 180 degrees: The angles cannot form a triangle. This would result in a shape where the lines would never meet to form a closed triangle. Imagine trying to form a triangle with angles of 100°, 90°, and 100°; the total is 290°, far exceeding the required 180°.
Types of Triangles Based on Angles
Understanding the types of triangles helps to visualize the angles and reinforces the 180-degree rule. Triangles are categorized into three main types based on their angles:
1. Acute Triangles
An acute triangle has all three angles measuring less than 90 degrees. The sum of these three acute angles, of course, must still equal 180 degrees. Example: 60°, 60°, 60° (an equilateral triangle is a special case of an acute triangle). Another example could be 45°, 70°, 65°.
2. Right Triangles
A right triangle contains one 90-degree angle (a right angle). The other two angles must be acute and add up to 90 degrees to satisfy the 180-degree rule. Example: 90°, 45°, 45°. Another example could be 90°, 30°, 60°.
3. Obtuse Triangles
An obtuse triangle has one angle greater than 90 degrees (an obtuse angle). The other two angles must be acute and their sum must be less than 90 degrees. Example: 100°, 40°, 40°. Another example is 120°, 30°, 30°.
Practical Applications and Examples
Let's apply the rules with some examples:
Example 1: Can the angles 50°, 60°, and 70° form a triangle?
Solution: 50° + 60° + 70° = 180°. Yes, these angles can form a triangle (an acute triangle).
Example 2: Can the angles 40°, 50°, and 100° form a triangle?
Solution: 40° + 50° + 100° = 190°. No, these angles cannot form a triangle. The sum exceeds 180°.
Example 3: Can the angles 20°, 30°, and 120° form a triangle?
Solution: 20° + 30° + 120° = 170°. No, these angles cannot form a triangle. The sum is less than 180°.
Example 4: Can the angles 35°, 55°, and 90° form a triangle?
Solution: 35° + 55° + 90° = 180°. Yes, these angles can form a triangle (a right-angled triangle).
Example 5 (Advanced): A triangle has angles x, 2x, and 3x. Find the value of x and determine the type of triangle.
Solution: x + 2x + 3x = 180° 6x = 180° x = 30°
Therefore, the angles are 30°, 60°, and 90°. This is a right-angled triangle.
Beyond the Basics: Exterior Angles
While we've focused on interior angles, it's important to briefly mention exterior angles. An exterior angle is formed by extending one side of the triangle. The exterior angle and its adjacent interior angle are supplementary (they add up to 180°). An important theorem states that the measure of an exterior angle of a triangle is equal to the sum of the measures of the two non-adjacent interior angles. This theorem provides an alternative way to verify the triangle angle sum theorem and solve problems involving unknown angles.
Troubleshooting Common Mistakes
- Units: Always ensure you're working with angles in the same units (degrees). Mixing degrees and radians will lead to incorrect results.
- Accuracy: When calculating, use precise measurements to avoid rounding errors that might lead to slightly off sums.
- Understanding the Implications: Don't just focus on the numerical sum; understand what the sum means in terms of the geometric shape it represents.
Conclusion: Mastering Triangle Angles
The ability to determine whether a set of angles can form a triangle is a fundamental skill in geometry. By mastering the Triangle Angle Sum Theorem and understanding the different types of triangles based on their angles, you’ll build a solid foundation for more advanced geometrical concepts. Remember to practice regularly, using a variety of examples, to solidify your understanding and enhance your problem-solving skills. This skill will serve you well in many areas, from further mathematics studies to practical applications in architecture, engineering, and design. The seemingly simple concept of triangle angles opens doors to a complex and fascinating world of geometric possibilities.
Latest Posts
Latest Posts
-
Glomerular Filtrate Is Least Likely To Contain
Apr 05, 2025
-
Find The Prime Factorization Of 27
Apr 05, 2025
-
Difference Between Operation And Production Management
Apr 05, 2025
-
Conclusion Of Millikan Oil Drop Experiment
Apr 05, 2025
-
Least Common Multiple 4 And 8
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Which Set Of Angles Can Form A Triangle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
