Which Of The Following Is An Example Of A Combination
Juapaving
Mar 28, 2025 · 6 min read
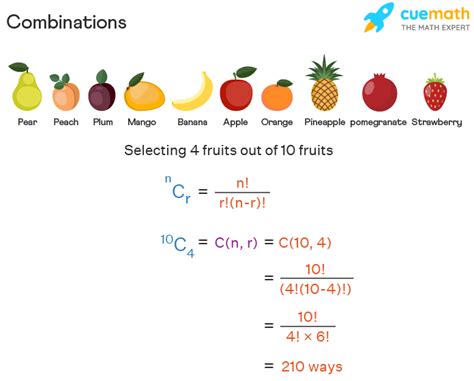
Table of Contents
Which of the Following is an Example of a Combination? Unlocking the Secrets of Combinatorics
The question, "Which of the following is an example of a combination?" might seem deceptively simple. However, understanding combinations requires delving into the fascinating world of combinatorics, a branch of mathematics that deals with counting and arranging objects. This article will explore what constitutes a combination, differentiate it from permutations, and provide numerous examples to solidify your understanding. We'll also touch upon the applications of combinations in various fields.
Understanding Combinations vs. Permutations
Before we delve into examples, let's clarify the crucial distinction between combinations and permutations. Both deal with selecting items from a set, but the key difference lies in whether the order of selection matters.
-
Permutations: In permutations, the order of selection is crucial. Selecting item A then item B is considered different from selecting item B then item A. Think of arranging books on a shelf – the order matters.
-
Combinations: In combinations, the order of selection is irrelevant. Selecting item A then item B is the same as selecting item B then item A. Think of choosing a committee – the order in which members are selected doesn't change the composition of the committee.
The formula for combinations is:
nCr = n! / (r! * (n-r)!)
Where:
- n is the total number of items in the set.
- r is the number of items being selected.
- ! denotes the factorial (e.g., 5! = 5 * 4 * 3 * 2 * 1).
Examples of Combinations: A Diverse Range of Applications
Now, let's explore a wide range of examples to illustrate the concept of combinations:
1. Selecting a Committee:
Imagine you need to form a committee of 3 people from a group of 10. The order in which you select the committee members doesn't matter; the same committee is formed regardless of the selection order. This is a classic example of a combination. Using the formula:
10C3 = 10! / (3! * 7!) = 120
There are 120 possible combinations of 3-person committees from a group of 10.
2. Choosing Lottery Numbers:
Lottery games often involve selecting a set of numbers from a larger pool. The order in which you pick the numbers doesn't affect your winnings; only the numbers themselves matter. This is another perfect example of a combination. For instance, if you choose 6 numbers out of 49, the number of possible combinations is:
49C6 = 49! / (6! * 43!) = 13,983,816
3. Dealing Cards in Poker:
In poker, the order in which you receive your cards doesn't change your hand's value. A hand of two aces and three kings remains the same whether the aces came first or last. Thus, calculating the number of possible five-card poker hands is a combination problem.
4. Selecting Flavors for Ice Cream:
If an ice cream shop offers 10 flavors and you want to choose 3 scoops, the order of scoops doesn't change the overall combination of flavors you enjoy. This is a combination.
5. Forming Subsets of a Set:
Consider a set of letters {A, B, C}. The possible combinations (subsets) of selecting 2 letters are: {A, B}, {A, C}, {B, C}. Notice that {A, B} is the same as {B, A} in a combination.
6. Selecting Items from a Menu:
If a restaurant offers 5 appetizers and you wish to choose 2, the order in which you choose them doesn't affect your meal. This is a combination problem.
7. Pizza Toppings:
Let's say a pizza place has 8 toppings. You can choose any number of toppings. How many different pizza combinations are possible? This is a classic combinations problem, but it involves understanding the concept of combinations with replacement (since you can choose the same topping multiple times). This introduces a slightly more complex formula but still falls under the umbrella of combinatorics.
8. Molecular Biology:
Combinations play a vital role in molecular biology. For instance, calculating the possible combinations of amino acids in a peptide chain of a specific length is a crucial combinatorial problem.
9. Computer Science:
In algorithm design and data structure analysis, combinatorial principles are frequently used to determine the efficiency and complexity of various computational approaches. The number of possible paths in a graph, for example, can be determined using combinatorial methods.
10. Cryptography:
Cryptography heavily relies on combinatorial mathematics. The strength of many encryption algorithms depends on the vast number of possible combinations of keys or passwords. The security of these systems hinges on the infeasibility of trying all possible combinations within a reasonable timeframe.
11. Project Management:
When selecting tasks for a project, combinations can be used to find the number of different ways the tasks can be grouped or sequenced, helping to optimize project timelines and resource allocation.
12. Sports:
In many sports, especially those with team selections, combinations are used to determine the number of possible team lineups. For instance, selecting a starting lineup in basketball or soccer involves using combinations to account for the number of players and positions.
Differentiating Combinations from Permutations: A Comparative Approach
To further solidify your understanding, let's compare combinations with permutations through specific scenarios:
Scenario: Choosing three students from a class of five to form a committee.
-
Combination: The order doesn't matter. Selecting students A, B, and C is the same as selecting students C, B, and A. The number of combinations is 5C3 = 10.
-
Permutation: The order matters. Selecting students A, B, and C is different from selecting students C, B, and A. The number of permutations is 5P3 = 60.
Scenario: Arranging three books on a shelf from a collection of five different books.
-
Combination: This is not a combination problem because the order in which the books are placed on the shelf is crucial.
-
Permutation: This is a permutation problem. The number of permutations is 5P3 = 60.
Beyond the Basics: Advanced Combinatorial Concepts
While the basic combination formula is sufficient for many applications, more advanced combinatorial concepts exist to handle more complex scenarios:
-
Combinations with Repetition: This allows selecting the same item multiple times. Think of choosing scoops of ice cream where you can choose the same flavor repeatedly.
-
Multinomial Coefficients: These extend the binomial theorem to situations involving more than two categories.
-
Generating Functions: These are powerful tools used to enumerate combinations and solve complex combinatorial problems.
Conclusion: Mastering the Art of Combinations
Understanding combinations is essential in various fields, from probability and statistics to computer science and project management. By mastering the concepts discussed here, you will have acquired a valuable toolset applicable to many real-world situations. Remember the key difference between combinations and permutations: order matters in permutations, but not in combinations. Practice working through various examples, and you will become confident in applying the principles of combinatorics to solve diverse problems. The world of combinations is vast and rewarding; keep exploring its possibilities!
Latest Posts
Latest Posts
-
2 Over 5 As A Percent
Mar 31, 2025
-
35 Inches Is How Many Feet
Mar 31, 2025
-
3 Cm Is How Many Mm
Mar 31, 2025
-
How Many Lines Of Symmetry Are In A Star
Mar 31, 2025
-
Which Of The Following Is An Ecosystem
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Which Of The Following Is An Example Of A Combination . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
