2 Over 5 As A Percent
Juapaving
Mar 31, 2025 · 5 min read
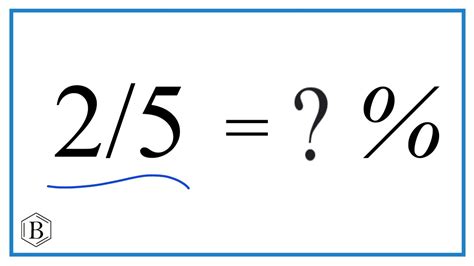
Table of Contents
2 Over 5 as a Percent: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics with widespread applications in everyday life. This comprehensive guide will delve into the conversion of the fraction 2/5 into a percentage, exploring various methods, practical examples, and related concepts. We'll also touch upon the broader context of fraction-to-percentage conversions and their importance.
Understanding Fractions and Percentages
Before diving into the conversion of 2/5 to a percentage, let's solidify our understanding of these fundamental concepts.
Fractions: A fraction represents a part of a whole. It consists of two parts: the numerator (the top number) and the denominator (the bottom number). The numerator indicates the number of parts being considered, while the denominator indicates the total number of equal parts that make up the whole. For example, in the fraction 2/5, 2 is the numerator and 5 is the denominator. This means we are considering 2 out of 5 equal parts.
Percentages: A percentage is a way of expressing a number as a fraction of 100. The symbol "%" is used to denote a percentage. For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Percentages are used extensively to represent proportions, rates, and changes in various contexts.
Converting 2/5 to a Percentage: Method 1 - The Direct Approach
The most straightforward way to convert 2/5 to a percentage is to understand that a percentage is simply a fraction with a denominator of 100. Therefore, we need to find an equivalent fraction of 2/5 that has 100 as its denominator.
To do this, we can set up a proportion:
2/5 = x/100
To solve for 'x', we cross-multiply:
5x = 200
Now, divide both sides by 5:
x = 40
Therefore, 2/5 is equal to 40/100, which is equivalent to 40%.
Converting 2/5 to a Percentage: Method 2 - Using Decimal Conversion
Another common method involves first converting the fraction to a decimal and then multiplying by 100 to obtain the percentage.
To convert 2/5 to a decimal, we simply divide the numerator (2) by the denominator (5):
2 ÷ 5 = 0.4
Now, multiply the decimal by 100 to express it as a percentage:
0.4 x 100 = 40
Therefore, 2/5 is equal to 40%. This method is particularly useful when dealing with fractions that don't easily convert to a fraction with a denominator of 100.
Real-World Applications of 2/5 as a Percent (40%)
Understanding the conversion of 2/5 to 40% has numerous practical applications in various fields:
-
Sales and Discounts: A store offering a 40% discount means customers pay only 60% (100% - 40%) of the original price. Imagine a shirt originally costing $50; the discount would be $20 (40% of $50), and the final price would be $30.
-
Surveys and Statistics: If a survey reveals that 2 out of every 5 people prefer a particular brand, this translates to a 40% preference rate for that brand. This information is crucial for marketing and product development strategies.
-
Financial Calculations: In finance, percentages are fundamental for calculating interest rates, returns on investment, and profit margins. Understanding 2/5 as 40% allows for quick calculations related to these areas. For instance, if you invest $1000 and it yields a 40% return, your profit would be $400.
-
Grades and Assessments: In education, scores are often expressed as percentages. If a student answers 2 out of 5 questions correctly on a quiz, they achieve a 40% score.
-
Recipe Scaling: When cooking, adjusting recipes often involves using percentages or fractions. If a recipe calls for 2/5 of a cup of sugar, you can easily calculate the amount needed (40% of the cup).
Further Exploration: Converting Other Fractions to Percentages
The methods described above can be applied to convert any fraction into a percentage. Let's look at a few examples:
-
1/4: 1 ÷ 4 = 0.25; 0.25 x 100 = 25%
-
3/4: 3 ÷ 4 = 0.75; 0.75 x 100 = 75%
-
1/2: 1 ÷ 2 = 0.5; 0.5 x 100 = 50%
-
3/5: 3 ÷ 5 = 0.6; 0.6 x 100 = 60%
-
7/10: 7 ÷ 10 = 0.7; 0.7 x 100 = 70%
Importance of Understanding Fraction-to-Percentage Conversions
The ability to seamlessly convert fractions to percentages, and vice versa, is a critical skill for various reasons:
-
Data Interpretation: Understanding percentages allows for quick comprehension and comparison of data presented in fractional form.
-
Problem-Solving: Many real-world problems involve the manipulation and calculation of fractions and percentages. Being fluent in both is essential for effective problem-solving.
-
Decision Making: Percentages provide a clear and concise way to present information for informed decision-making.
-
Communication: Using percentages often makes information more easily understood and communicated to a wider audience.
Advanced Concepts and Applications
Beyond the basics, understanding fraction-to-percentage conversions opens doors to more advanced mathematical concepts and applications:
-
Calculating Percentages of Percentages: This involves working with nested percentages, which are crucial in compound interest calculations and other financial applications.
-
Percentage Change and Percentage Increase/Decrease: These calculations are frequently used to analyze changes over time and to compare data across different periods.
-
Statistical Analysis: Percentages are extensively used in statistical analyses to represent proportions, probabilities, and trends.
Conclusion
Converting 2/5 to a percentage, resulting in 40%, is a seemingly simple task, yet it underpins a significant portion of mathematical applications in our daily lives. Mastering this conversion, along with the broader understanding of fractions and percentages, equips you with the essential tools for interpreting data, solving problems, and making informed decisions across diverse fields. The ability to readily convert fractions to percentages empowers you to confidently navigate various aspects of your personal and professional life. From calculating discounts and understanding statistical data to scaling recipes and grasping financial concepts, this skill proves invaluable. Remember to practice regularly to solidify your understanding and enhance your computational speed and accuracy.
Latest Posts
Latest Posts
-
Cold B Lood Vs Cold Heart
Apr 01, 2025
-
Lowest Common Denominator Of 12 And 9
Apr 01, 2025
-
What Is The Advantage Of A Four Chambered Heart
Apr 01, 2025
-
Endocrine Glands Are Often Called Ducted Glands True False
Apr 01, 2025
-
Where Does Sound Waves Travel Fastest
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about 2 Over 5 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
