Which Is Bigger 3/8 Or 1/2
Juapaving
Mar 30, 2025 · 5 min read
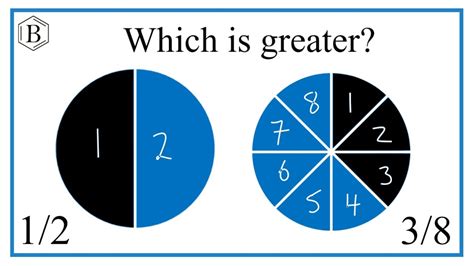
Table of Contents
Which is Bigger: 3/8 or 1/2? A Deep Dive into Fraction Comparison
Determining which fraction is larger, 3/8 or 1/2, might seem trivial at first glance. However, understanding the underlying principles of fraction comparison is crucial for mastering fundamental arithmetic and lays the groundwork for more advanced mathematical concepts. This comprehensive guide will not only answer the question definitively but will also explore various methods for comparing fractions, equipping you with the skills to confidently tackle similar problems in the future.
Understanding Fractions: A Quick Refresher
Before diving into the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two key components:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 3/8, the numerator is 3 (we have 3 parts) and the denominator is 8 (the whole is divided into 8 equal parts). Similarly, in the fraction 1/2, the numerator is 1, and the denominator is 2.
Method 1: Finding a Common Denominator
This is arguably the most common and straightforward method for comparing fractions. The goal is to rewrite both fractions so they share the same denominator. This allows for a direct comparison of their numerators.
Steps:
-
Find the Least Common Multiple (LCM): Determine the least common multiple of the denominators (8 and 2 in this case). The LCM of 8 and 2 is 8.
-
Rewrite the Fractions: Convert both fractions to equivalent fractions with the LCM as the denominator.
-
For 3/8, the denominator is already 8, so it remains unchanged.
-
For 1/2, to get a denominator of 8, we multiply both the numerator and the denominator by 4: (1 x 4) / (2 x 4) = 4/8
-
-
Compare the Numerators: Now that both fractions have the same denominator (8), we can compare their numerators: 3 and 4. Since 4 > 3, we conclude that 4/8 > 3/8.
Therefore, 1/2 > 3/8
Method 2: Converting to Decimals
Another effective method involves converting both fractions into their decimal equivalents. This approach is particularly useful when dealing with fractions that are difficult to convert to a common denominator.
Steps:
-
Divide the Numerator by the Denominator: For each fraction, divide the numerator by the denominator.
-
For 3/8: 3 ÷ 8 = 0.375
-
For 1/2: 1 ÷ 2 = 0.5
-
-
Compare the Decimals: Now compare the decimal values: 0.5 and 0.375. Since 0.5 > 0.375, we conclude that 1/2 > 3/8.
Therefore, 1/2 > 3/8
Method 3: Visual Representation
Visual aids can be incredibly helpful, especially for beginners. Imagine a circle (or any shape) divided into equal parts.
-
1/2: Divide the circle into two equal halves. 1/2 represents one of those halves.
-
3/8: Divide the circle into eight equal parts. 3/8 represents three of those eight parts.
By visually comparing the shaded portions representing 1/2 and 3/8, it becomes clear that the area representing 1/2 is larger than the area representing 3/8.
Therefore, 1/2 > 3/8
Why Understanding Fraction Comparison is Important
The ability to compare fractions is fundamental to various mathematical operations and real-world applications. Here are a few examples:
-
Baking and Cooking: Following recipes often requires understanding and comparing fractions of ingredients.
-
Construction and Engineering: Precise measurements and calculations in construction and engineering rely heavily on fraction comparison.
-
Data Analysis: Comparing proportions and percentages, which are essentially fractions, is crucial for analyzing data effectively.
-
Finance: Understanding fractions and their comparison is essential for working with percentages, interest rates, and other financial calculations.
-
Advanced Mathematics: Fraction comparison forms the basis for more advanced concepts like ratios, proportions, and algebraic equations.
Beyond the Basics: More Complex Fraction Comparisons
While the methods discussed above are suitable for comparing simple fractions, more complex scenarios might arise. Let's explore some of these:
-
Fractions with Different Denominators and Numerators: The common denominator method remains the most reliable approach in these cases.
-
Mixed Numbers: Mixed numbers (a whole number and a fraction, like 1 1/4) require converting them into improper fractions before applying the comparison methods. For example, 1 1/4 becomes 5/4.
-
Comparing More Than Two Fractions: In such cases, convert all fractions to a common denominator and compare their numerators. The fraction with the largest numerator is the largest.
Tips and Tricks for Efficient Fraction Comparison
-
Memorize Common Fraction Equivalents: Knowing that 1/2 = 2/4 = 4/8 = 5/10, etc., can significantly speed up the comparison process.
-
Simplify Fractions Before Comparing: Simplifying fractions to their lowest terms makes the comparison process easier. For example, comparing 6/12 and 3/8 is easier after simplifying 6/12 to 1/2.
-
Use a Calculator (When Appropriate): While understanding the underlying principles is crucial, using a calculator to convert fractions to decimals can save time, especially for complex fractions.
-
Practice Regularly: The key to mastering fraction comparison, like any mathematical skill, is consistent practice.
Conclusion: Mastering the Art of Fraction Comparison
Determining whether 3/8 or 1/2 is larger is a simple yet fundamental exercise in understanding fractions. By mastering the techniques of finding common denominators, converting to decimals, and utilizing visual representations, you build a strong foundation in fraction comparison. This skill extends far beyond basic arithmetic, proving invaluable across numerous academic disciplines and real-world applications. Remember, consistent practice and a thorough understanding of the principles involved are key to becoming proficient in this essential mathematical skill. Continue practicing and exploring different fraction comparison problems to further solidify your understanding and confidence.
Latest Posts
Latest Posts
-
What Is The Lcm Of 4 5 And 8
Apr 01, 2025
-
Differentiate Between Leading Strand And Lagging Strand
Apr 01, 2025
-
Measure Of The Quantity Of Matter
Apr 01, 2025
-
What Is The Multiple Of 15
Apr 01, 2025
-
The Proper Electron Dot Symbol For Aluminum Is
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Which Is Bigger 3/8 Or 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
