What's The Square Root Of 41
Juapaving
Apr 05, 2025 · 5 min read
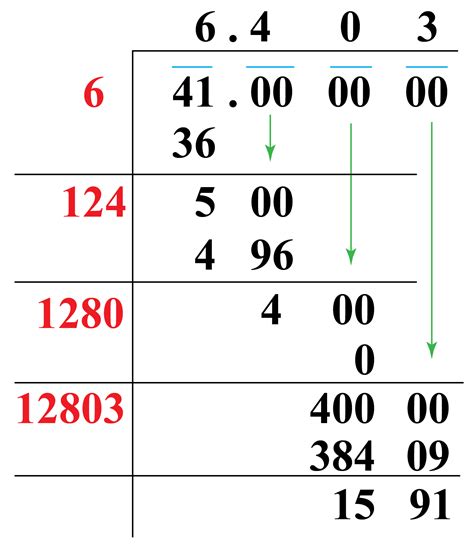
Table of Contents
What's the Square Root of 41? A Deep Dive into Irrational Numbers and Approximation Techniques
The seemingly simple question, "What's the square root of 41?", opens a fascinating window into the world of mathematics, specifically the realm of irrational numbers and the various methods used to approximate their values. While a precise answer isn't expressible as a simple fraction or terminating decimal, understanding how we approach this problem unveils powerful mathematical concepts and techniques.
Understanding Square Roots
Before delving into the specifics of the square root of 41, let's establish a foundational understanding of square roots. The square root of a number, denoted as √x, is a value that, when multiplied by itself, equals x. For example, the square root of 9 (√9) is 3 because 3 * 3 = 9. This concept is fundamental to various areas of mathematics, physics, and engineering.
Why 41 is Special: Irrational Numbers
Unlike the square root of 9, the square root of 41 (√41) is an irrational number. This means it cannot be expressed as a simple fraction (a ratio of two integers). Its decimal representation is non-terminating and non-repeating, extending infinitely without ever settling into a predictable pattern. This characteristic distinguishes it from rational numbers like 0.5 (1/2) or 0.75 (3/4).
The irrationality of √41 stems from the fact that 41 is not a perfect square. A perfect square is a number that results from squaring an integer (e.g., 1, 4, 9, 16, 25, etc.). Since no integer multiplied by itself equals 41, its square root is irrational.
Methods for Approximating √41
Since we cannot express √41 exactly, we must resort to approximation techniques. Several methods exist, each offering varying levels of accuracy and complexity.
1. Guess and Check Method
This is the most basic approach. We start by guessing a number and then square it to see how close it is to 41. If our guess is too low, we increase it; if it's too high, we decrease it. We iterate this process until we reach a satisfactory level of accuracy.
For example:
- 6² = 36 (too low)
- 7² = 49 (too high)
This tells us that √41 lies between 6 and 7. We can refine our guess further:
- 6.4² = 40.96 (very close!)
- 6.403² ≈ 41.00 (even closer!)
This method, while intuitive, is not very efficient for high levels of accuracy.
2. Babylonian Method (Heron's Method)
This iterative method provides a much more efficient way to approximate square roots. It's based on a recursive formula:
x_(n+1) = 0.5 * (x_n + a/x_n)
where:
- x_n is the current approximation
- x_(n+1) is the next approximation
- a is the number whose square root we want to find (in our case, 41)
Let's apply it:
- Initial Guess: Let's start with x_0 = 6.
- Iteration 1: x_1 = 0.5 * (6 + 41/6) ≈ 6.4167
- Iteration 2: x_2 = 0.5 * (6.4167 + 41/6.4167) ≈ 6.4031
- Iteration 3: x_3 = 0.5 * (6.4031 + 41/6.4031) ≈ 6.4031
As you can see, the Babylonian method converges to the true value very quickly. After just a few iterations, we have a highly accurate approximation.
3. Using a Calculator or Computer
Modern calculators and computer software readily provide highly accurate approximations of square roots. Simply input √41 and the calculator will output a decimal approximation, often to many decimal places.
4. Taylor Series Expansion
For those comfortable with calculus, the Taylor series expansion provides a powerful method to approximate functions, including square roots. The Taylor series expansion for √(1+x) around x=0 is:
√(1+x) ≈ 1 + x/2 - x²/8 + x³/16 - ...
To use this for √41, we rewrite 41 as 36(1 + 5/36) and let x = 5/36. While this method is more mathematically involved, it offers a high degree of accuracy.
The Importance of Approximation
The inability to express √41 exactly as a decimal or fraction highlights the richness of the number system. Irrational numbers are ubiquitous in mathematics and the physical world. Approximation techniques are crucial because they enable us to work with these numbers in practical applications. Engineers, physicists, and computer scientists routinely use approximation methods to solve problems involving irrational numbers.
√41 in Real-World Applications
While it might seem like a purely theoretical exercise, understanding and approximating √41 has tangible applications. Consider these examples:
- Geometry and Trigonometry: Calculating the diagonal of a rectangle with sides of a specific length may involve the square root of a non-perfect square.
- Physics: Many physical formulas involve square roots, for example, in calculations involving velocity, energy, or distance.
- Computer Graphics: Rendering and animation frequently require calculations involving square roots for accurate representation of shapes and movements.
Conclusion: Embracing the Irrational
The question "What's the square root of 41?" transcends a simple numerical answer. It's a gateway to exploring the fascinating world of irrational numbers and the ingenuity of approximation techniques. Understanding these concepts is fundamental to numerous scientific and mathematical disciplines, highlighting the practical importance of seemingly abstract mathematical ideas. While we can't express √41 precisely, we can approximate it with remarkable accuracy using various methods, allowing us to utilize it in practical calculations and problem-solving. The pursuit of accuracy, even in the face of an irrational number, showcases the power and elegance of mathematics. The journey to understanding √41 is as important as the destination, offering insights into the nature of numbers and the methods we employ to understand them.
Latest Posts
Latest Posts
-
Which Of The Following Is Correct
Apr 06, 2025
-
800 Square Meters In Square Feet
Apr 06, 2025
-
Buffer Region On A Titration Curve
Apr 06, 2025
-
What Is The Relationship Between Kinetic And Potential Energy
Apr 06, 2025
-
Conversion Of Mechanical Energy To Electrical Energy
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about What's The Square Root Of 41 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
