What's The Square Root Of 125
Juapaving
Mar 26, 2025 · 6 min read
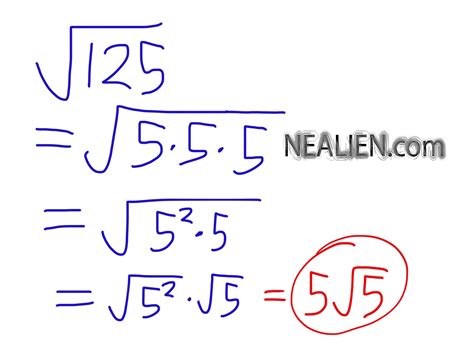
Table of Contents
Decoding the Square Root of 125: A Deep Dive into Methods and Applications
Finding the square root of 125 might seem like a simple mathematical exercise, but it opens a door to a fascinating world of mathematical concepts and practical applications. This article will explore various methods for calculating the square root of 125, delve into its significance in different fields, and examine related mathematical ideas. We'll go beyond just providing the answer; we'll understand why the answer is what it is and how this seemingly simple calculation underpins more complex mathematical operations.
Understanding Square Roots: A Fundamental Concept
Before we dive into the specifics of √125, let's refresh our understanding of square roots. The square root of a number (x) is a value that, when multiplied by itself, equals x. In simpler terms, it's the inverse operation of squaring a number. For example, the square root of 9 (√9) is 3, because 3 * 3 = 9.
This concept is fundamental in various mathematical fields, including algebra, geometry, and calculus. It's essential for solving equations, calculating distances, and understanding geometric shapes.
Methods for Calculating √125
There are several ways to calculate the square root of 125. Let's explore a few:
1. Prime Factorization Method:
This method involves breaking down the number into its prime factors. The prime factorization of 125 is 5 x 5 x 5, or 5³.
Therefore, √125 = √(5³). We can simplify this as follows: √(5³)= √(5² * 5) = 5√5. This gives us the exact value, expressing the square root as a product of an integer and a radical. This is often preferred in mathematical contexts where precision is paramount.
2. Long Division Method:
While less common in the age of calculators, the long division method provides a manual way to approximate the square root. This method involves a series of iterative steps, progressively refining the approximation until a desired level of accuracy is achieved. While detailed explanation requires a significant amount of space and would be best served with visual aids, numerous resources are available online that detail this method step-by-step. The method involves grouping digits, finding initial estimates, and successively refining the approximation through subtraction and division.
3. Using a Calculator:
The most straightforward and efficient method for finding the square root of 125 is using a calculator. Simply input 125 and press the square root button (√). The calculator will provide an approximate decimal value. Most calculators will display a value of approximately 11.180339887498949. This is a useful method for practical applications where a precise, decimal approximation is sufficient.
4. Newton-Raphson Method:
This is a powerful iterative method for finding the roots of equations. It's particularly useful for finding square roots, and it converges quickly to a highly accurate solution. This method is beyond the scope of this basic explanation, but it is a highly sophisticated method for numerical approximation that is used widely in computational mathematics and computer science.
Understanding the Decimal Approximation: 11.1803...
The decimal approximation of √125 (approximately 11.1803) is frequently used in practical scenarios where an exact value isn't strictly necessary. This approximate value allows for quick calculations and estimations in various real-world applications. It’s important to remember that this is only an approximation, and the actual value extends infinitely with no repeating pattern.
Applications of the Square Root of 125
The square root of 125, whether expressed as its exact value (5√5) or its approximate decimal value, finds application in numerous fields:
1. Geometry and Trigonometry:
The square root often appears in calculations involving distance, area, and volume. For instance, calculating the diagonal of a rectangle or the hypotenuse of a right-angled triangle may involve a square root calculation where the result is similar to √125.
2. Physics and Engineering:
Many physical phenomena are described by equations involving square roots. For example, the period of a pendulum or the velocity of an object under the influence of gravity can involve square roots in their mathematical formulations. Engineering projects that involve calculating forces, speeds, or distances frequently involve this fundamental calculation.
3. Statistics and Probability:
Square roots are crucial in statistical calculations, particularly in standard deviation and variance, providing measures of data dispersion. Many statistical analyses involve the calculation of square roots for the purposes of normalizing data and performing other calculations.
4. Computer Graphics and Game Development:
The square root calculation is ubiquitous in computer graphics and game development. For instance, calculating distances between points on a screen or within a game world invariably involves calculating square roots using the Pythagorean theorem or more complex vector calculations. Performance in these applications requires highly optimized square root algorithms.
5. Financial Modeling:
In finance, calculations involving compound interest or investment growth often include square roots in their mathematical models.
Beyond the Basics: Exploring Related Concepts
Understanding the square root of 125 provides a springboard to explore more complex mathematical concepts:
1. Irrational Numbers:
The square root of 125 is an example of an irrational number – a number that cannot be expressed as a simple fraction (a ratio of two integers). Irrational numbers have an infinite, non-repeating decimal expansion.
2. Radical Expressions:
The expression 5√5 is a radical expression, which involves a root symbol (√). Simplifying radical expressions is a fundamental skill in algebra.
3. Approximating Irrational Numbers:
Various methods exist for approximating irrational numbers, including the use of Taylor series and continued fractions. These methods are used in computer science and numerical analysis to obtain efficient and accurate approximations.
4. Complex Numbers:
The concept of square roots extends to complex numbers, which involve the imaginary unit 'i' (√-1).
5. Higher-Order Roots:
The square root is a special case of higher-order roots (cube roots, fourth roots, etc.). These higher-order roots are essential in advanced mathematical topics like algebra and number theory.
Conclusion: The Significance of a Seemingly Simple Calculation
The calculation of the square root of 125, while seemingly simple at first glance, reveals a wealth of underlying mathematical principles and practical applications. From the fundamental concept of square roots to their applications across various disciplines, understanding this calculation illuminates the interconnectedness of mathematics and its essential role in our world. The methods for calculating √125, from prime factorization to sophisticated numerical techniques, illustrate the diverse approaches mathematicians and computer scientists employ to tackle such fundamental problems. Moreover, exploring related concepts like irrational numbers and radical expressions deepens our understanding of the broader mathematical landscape. Therefore, even a seemingly simple mathematical operation like finding the square root of 125 opens doors to a rich and rewarding exploration of mathematics.
Latest Posts
Latest Posts
-
1800 In Words For A Check
Mar 29, 2025
-
What Is The Lcm Of 5 6 And 7
Mar 29, 2025
-
How Much Valence Electrons Does Oxygen Have
Mar 29, 2025
-
What Percent Of 80 Is 12
Mar 29, 2025
-
Least Common Multiple Of 6 7 And 8
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about What's The Square Root Of 125 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
