Quadrilateral With One Pair Of Parallel Sides
Juapaving
Apr 03, 2025 · 5 min read
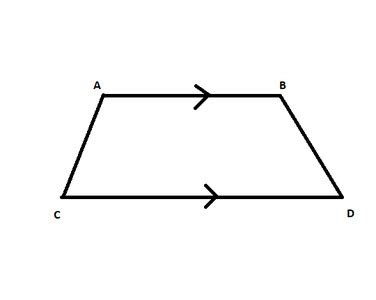
Table of Contents
Quadrilaterals with One Pair of Parallel Sides: A Deep Dive into Trapezoids
Quadrilaterals, four-sided polygons, encompass a diverse family of shapes. Among them, a particularly interesting group is defined by the presence of just one pair of parallel sides. These shapes are known as trapezoids (or trapeziums, depending on your regional convention). This article will delve deep into the fascinating world of trapezoids, exploring their properties, classifications, area calculations, and applications.
Understanding Trapezoids: Definition and Basic Properties
A trapezoid (or trapezium) is a quadrilateral with at least one pair of parallel sides. These parallel sides are called bases, while the other two sides are called legs or lateral sides. It's crucial to understand that the definition only requires at least one pair of parallel sides. This means that a parallelogram, with its two pairs of parallel sides, is technically a special case of a trapezoid.
Here's a breakdown of key properties:
- Parallel Sides: The defining characteristic of a trapezoid is its at least one pair of parallel sides, the bases.
- Non-Parallel Sides: The legs or lateral sides are not necessarily parallel or equal in length.
- Angles: Adjacent angles along the same leg are supplementary (their sum is 180 degrees). This is a direct consequence of the parallel lines and transversals formed by the bases and legs.
- Diagonals: The diagonals of a trapezoid intersect, but generally do not bisect each other (unlike in parallelograms).
Distinguishing Trapezoids from Parallelograms and Other Quadrilaterals
It's important to clearly differentiate trapezoids from other quadrilaterals:
- Parallelograms: Parallelograms possess two pairs of parallel sides. Trapezoids only have one. Therefore, all parallelograms are trapezoids, but not all trapezoids are parallelograms.
- Rectangles, Rhombuses, Squares: These are all special cases of parallelograms, and consequently, also special cases of trapezoids.
- Kites: Kites have two pairs of adjacent sides that are equal in length, but their sides aren't necessarily parallel. They are distinct from trapezoids.
- Irregular Quadrilaterals: Any quadrilateral that doesn't fit the criteria of a parallelogram, trapezoid, kite, or other specific quadrilateral types falls under the category of irregular quadrilaterals.
Classifications of Trapezoids
Trapezoids can be further categorized based on their properties:
1. Isosceles Trapezoids
An isosceles trapezoid is a trapezoid where the legs are congruent (equal in length). This leads to some additional interesting properties:
- Base Angles: The base angles (angles at the ends of each base) are congruent. This means that the angles at the ends of one base are equal to each other, and similarly for the angles at the ends of the other base.
- Diagonals: The diagonals of an isosceles trapezoid are congruent (equal in length).
2. Right Trapezoids
A right trapezoid is a trapezoid where at least one leg is perpendicular to both bases. This results in right angles at the intersection points of the legs and bases. Right trapezoids provide a relatively straightforward approach to calculating their areas.
3. Scalene Trapezoids
A scalene trapezoid is a trapezoid where all sides have different lengths. It's the most general type of trapezoid, lacking the special symmetries of isosceles or right trapezoids.
Calculating the Area of a Trapezoid
The area of a trapezoid is calculated using a simple formula:
Area = (1/2) * (sum of bases) * height
Where:
- Bases: The lengths of the two parallel sides.
- Height: The perpendicular distance between the two parallel sides.
Example Calculation
Let's say a trapezoid has bases of length 5 cm and 9 cm, and a height of 4 cm. The area would be:
Area = (1/2) * (5 cm + 9 cm) * 4 cm = 28 cm²
This formula works for all types of trapezoids – isosceles, right, or scalene. The key is to accurately measure or calculate the lengths of the bases and the perpendicular height.
Advanced Properties and Theorems
Beyond the basics, several more advanced theorems and properties relate to trapezoids:
Midsegment Theorem
The midsegment of a trapezoid is the line segment connecting the midpoints of the two legs. The midsegment theorem states that the length of the midsegment is equal to the average of the lengths of the bases. This is a useful property for calculating unknown lengths within a trapezoid.
Area Using Coordinate Geometry
If you know the coordinates of the vertices of a trapezoid, you can use the determinant method or the shoelace formula from coordinate geometry to calculate the area. This is particularly useful when dealing with trapezoids defined in a coordinate system.
Relationships with Other Shapes
As mentioned earlier, trapezoids have close relationships with other quadrilaterals. Understanding these relationships provides a richer understanding of geometrical properties and proofs. For instance, the properties of isosceles trapezoids are often proven using congruent triangles and parallel lines.
Applications of Trapezoids in Real World
Trapezoids, despite not being as prominently featured as squares or rectangles in basic geometry, are frequently found in the real world:
- Architecture: Trapezoidal shapes are found in architectural designs, such as window frames, roof supports, and building foundations. The stability offered by the parallel base structure is advantageous in construction.
- Engineering: Trapezoidal cross-sections are common in beams and other structural elements. The geometry provides a balance between strength and material efficiency.
- Art and Design: Trapezoids are used in artistic compositions and graphic design, providing visual interest and dynamic forms.
- Nature: Many natural formations, such as certain rock formations and crystalline structures, exhibit trapezoidal shapes.
Solving Problems Involving Trapezoids
Many geometry problems involve trapezoids, testing your understanding of their properties and theorems. These problems can range from simple area calculations to more complex proofs involving congruent triangles and similar figures. Mastering these problem-solving skills is essential for success in geometry and related fields.
Example Problem:
A trapezoid has bases of length 8 cm and 12 cm. The area of the trapezoid is 60 cm². Find the height of the trapezoid.
Solution:
Using the area formula:
60 cm² = (1/2) * (8 cm + 12 cm) * height
Solving for the height, we find the height to be 6 cm.
Conclusion: A Comprehensive Overview
Trapezoids, while often overshadowed by other quadrilaterals, possess a unique set of properties and play a significant role in various applications. Understanding their definition, classifications, area calculations, and advanced properties is crucial for anyone interested in geometry, engineering, architecture, or related fields. This comprehensive guide has provided a detailed exploration of trapezoids, equipping you with the knowledge and skills to tackle any problem involving these fascinating shapes. From the simple area calculation to more complex theorems, the world of trapezoids offers a wealth of geometrical insights.
Latest Posts
Latest Posts
-
How Many Meter Is 10 Feet
Apr 04, 2025
-
What Lays Eggs And Is Not A Bird
Apr 04, 2025
-
An Alternate Form Of A Gene
Apr 04, 2025
-
How Many Joules In A Kilowatt Hour
Apr 04, 2025
-
1 Nucleic Acids Are Polymers Of
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Quadrilateral With One Pair Of Parallel Sides . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
