What Is The Sum Of Exterior Angles Of A Pentagon
Juapaving
Mar 21, 2025 · 5 min read
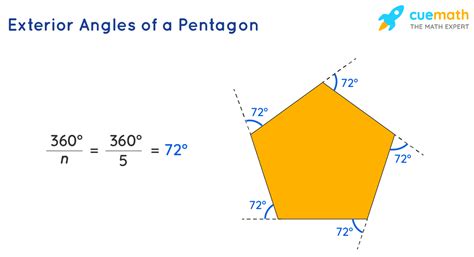
Table of Contents
What is the Sum of Exterior Angles of a Pentagon? A Deep Dive into Geometry
Understanding the properties of polygons, especially the sum of their exterior angles, is fundamental to geometry. This article delves deep into the concept, focusing specifically on pentagons, while also providing a broader understanding applicable to other polygons. We'll explore the concept, prove the theorem, solve problems, and even touch upon real-world applications.
Understanding Polygons and Their Angles
Before we focus on pentagons, let's establish a solid foundation. A polygon is a closed two-dimensional figure formed by connecting line segments. These line segments are called sides, and the points where they meet are called vertices. Polygons are classified based on the number of sides they have:
- Triangle: 3 sides
- Quadrilateral: 4 sides
- Pentagon: 5 sides
- Hexagon: 6 sides
- Heptagon: 7 sides
- and so on...
Polygons have two types of angles:
- Interior Angles: These are the angles formed inside the polygon at each vertex.
- Exterior Angles: These are the angles formed outside the polygon by extending one side at each vertex. For each vertex, there are two exterior angles – we typically focus on the exterior angle that is supplementary (adds up to 180°) to the interior angle.
The Sum of Exterior Angles: A Universal Theorem
A crucial theorem in geometry states that the sum of the exterior angles of any polygon, one at each vertex, is always 360 degrees. This holds true regardless of the number of sides the polygon has – whether it's a triangle, a quadrilateral, a pentagon, or a polygon with hundreds of sides.
This theorem is remarkably consistent and offers a powerful tool for solving various geometric problems. Let's explore why this is true.
Proving the Theorem: A Visual and Logical Approach
Imagine walking around the perimeter of any polygon. At each vertex, you make a turn. The exterior angle represents the amount you turn at each vertex. When you complete your walk and return to your starting point, you will have made a complete 360-degree turn. This visual representation provides an intuitive understanding of why the sum of exterior angles is always 360°.
A more formal proof can be achieved using mathematical induction, but the visual approach effectively conveys the core concept.
Focusing on Pentagons: A Deeper Dive
Now, let's apply this understanding specifically to pentagons. A pentagon, as mentioned earlier, is a polygon with five sides and five vertices. Therefore, it also has five interior angles and five exterior angles.
Since the sum of the exterior angles of any polygon is 360 degrees, the sum of the exterior angles of a pentagon is also 360 degrees. This remains true regardless of the shape of the pentagon – whether it's regular (all sides and angles are equal) or irregular (sides and angles are of different lengths and measures).
Solving Problems Involving Pentagon Exterior Angles
Let's consider some examples to solidify our understanding:
Example 1: Finding an Unknown Exterior Angle
Suppose a pentagon has four exterior angles measuring 70°, 80°, 60°, and 50°. What is the measure of the fifth exterior angle?
Solution:
We know the sum of the exterior angles is 360°. Therefore:
70° + 80° + 60° + 50° + x = 360°
260° + x = 360°
x = 360° - 260°
x = 100°
The fifth exterior angle measures 100°.
Example 2: Regular Pentagon Exterior Angles
A regular pentagon has all its sides and angles equal. What is the measure of each exterior angle?
Solution:
Since a regular pentagon has five equal exterior angles, we can divide the total sum of exterior angles (360°) by the number of angles (5):
360° / 5 = 72°
Each exterior angle of a regular pentagon measures 72°.
Example 3: Relationship between Interior and Exterior Angles
In a pentagon, one interior angle measures 100°. What is the measure of its corresponding exterior angle?
Solution:
Interior and exterior angles at the same vertex are supplementary, meaning they add up to 180°. Therefore:
180° - 100° = 80°
The corresponding exterior angle measures 80°.
Beyond Pentagons: Extending the Concept
The theorem regarding the sum of exterior angles applies to all polygons, not just pentagons. For instance:
- Triangle: The sum of exterior angles is 360°.
- Quadrilateral: The sum of exterior angles is 360°.
- Hexagon: The sum of exterior angles is 360°.
- Any n-sided polygon: The sum of exterior angles is 360°.
This consistency makes this theorem a cornerstone of geometry, providing a valuable tool for solving a wide range of problems involving polygons.
Real-World Applications of Exterior Angles
While the concept might seem purely theoretical, understanding exterior angles has practical applications in various fields:
- Architecture and Design: Architects and designers utilize geometric principles, including exterior angles, when designing buildings, bridges, and other structures. Understanding these angles ensures stability and aesthetic appeal.
- Engineering: Engineers use geometrical calculations, including those involving exterior angles, in designing mechanical systems, robotics, and various other engineering projects.
- Cartography: Mapmakers use geometrical principles to accurately represent geographical features. Understanding polygon properties aids in map projection and scaling.
- Computer Graphics and Game Development: Creating realistic and accurate 3D models and animations in computer games and graphics requires a strong foundation in geometry, including knowledge of polygon exterior angles.
Conclusion: Mastering Pentagon Exterior Angles and Beyond
Understanding the sum of the exterior angles of a pentagon, and polygons in general, is a critical concept in geometry. The fact that this sum always equals 360 degrees, regardless of the polygon's shape or size, provides a powerful and consistent tool for solving various geometric problems. From academic exercises to real-world applications in architecture, engineering, and other fields, grasping this concept offers a valuable skill set. The examples provided illustrate how to apply this knowledge effectively, paving the way for a deeper exploration of geometric principles and their practical significance. Remember, the key is not just memorizing the theorem but truly understanding its underlying logic and its wide-ranging applicability.
Latest Posts
Latest Posts
-
Hollow Spherical Shell Moment Of Inertia
Mar 28, 2025
-
173 9 Rounded To The Nearest Tenth
Mar 28, 2025
-
A Person Whose Height Is 6 Feet
Mar 28, 2025
-
What Are The Factor Of 24
Mar 28, 2025
-
List Three Physical Properties Of Ionic Compounds
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about What Is The Sum Of Exterior Angles Of A Pentagon . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
