Hollow Spherical Shell Moment Of Inertia
Juapaving
Mar 28, 2025 · 5 min read
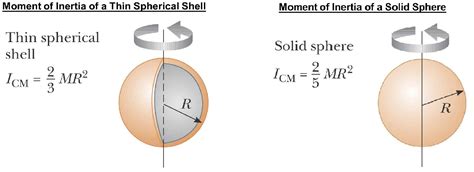
Table of Contents
Hollow Spherical Shell Moment of Inertia: A Comprehensive Guide
The moment of inertia, a crucial concept in physics and engineering, describes an object's resistance to changes in its rotation. For a hollow spherical shell, calculating this value requires a nuanced understanding of integral calculus and geometrical considerations. This comprehensive guide will delve into the intricacies of calculating the moment of inertia of a hollow spherical shell, exploring various approaches and providing a thorough understanding of the underlying principles.
Understanding Moment of Inertia
Before diving into the specifics of a hollow spherical shell, let's establish a foundational understanding of moment of inertia. Essentially, it's a measure of how difficult it is to change an object's rotational speed. A higher moment of inertia indicates a greater resistance to changes in angular velocity. This property depends on both the mass of the object and how that mass is distributed relative to the axis of rotation. The farther the mass is from the axis, the greater the moment of inertia.
Think of it like this: It's easier to spin a pencil than a bowling ball, even if they weigh the same. The bowling ball's mass is distributed farther from its center, resulting in a much larger moment of inertia.
The general formula for moment of inertia (I) is:
I = Σ mᵢrᵢ²
where:
mᵢis the mass of each individual particle in the objectrᵢis the distance of each particle from the axis of rotation- The summation (Σ) implies adding the contributions of all particles.
For continuous objects like a hollow spherical shell, we replace the summation with an integral.
Deriving the Moment of Inertia for a Hollow Spherical Shell
Calculating the moment of inertia for a hollow spherical shell involves integrating over the shell's surface. We'll focus on the moment of inertia about an axis passing through the center of the sphere (the most common scenario). The derivation involves several steps:
1. Defining the System
Consider a hollow spherical shell with a uniform mass density (ρ) and radius (R). We'll use spherical coordinates (r, θ, φ) to describe points on the shell's surface. The radius 'r' will be constant and equal to 'R'.
2. Determining a Mass Element (dm)
We need to define a small mass element (dm) on the shell's surface. This can be done using the surface area element in spherical coordinates:
dA = R²sin(θ)dθdφ
The mass density (ρ) is mass per unit area, so the mass element (dm) is:
dm = ρdA = ρR²sin(θ)dθdφ
3. Calculating the Moment of Inertia (I)
The moment of inertia (I) is the integral of the square of the distance (r²) from the axis of rotation multiplied by the mass element (dm):
I = ∫∫ r² dm = ∫∫ R² (ρR²sin(θ)dθdφ)
Since 'r' is always equal to 'R' in this case (it's on the surface of the sphere), we can simplify the equation:
I = ρR⁴ ∫₀²π ∫₀ᴨ sin(θ)dθdφ
4. Evaluating the Integral
The integral can be separated and solved easily:
I = ρR⁴ [∫₀²π dφ] [∫₀ᴨ sin(θ)dθ]
Solving the integrals:
∫₀²π dφ = 2π
∫₀ᴨ sin(θ)dθ = [-cos(θ)]₀ᴨ = 2
Therefore:
I = ρR⁴ (2π)(2) = 4πρR⁴
5. Expressing I in Terms of Total Mass (M)
The total mass (M) of the hollow spherical shell is the product of the density (ρ) and the surface area (4πR²):
M = ρ(4πR²)
We can solve for ρ:
ρ = M/(4πR²)
Substitute this back into the equation for I:
I = 4π[(M/(4πR²))]R⁴ = (2/3)MR²
Therefore, the moment of inertia of a hollow spherical shell about an axis through its center is (2/3)MR².
Parallel Axis Theorem
The parallel axis theorem provides a convenient method for calculating the moment of inertia about an axis parallel to the one passing through the center of mass. If you need to find the moment of inertia about an axis that doesn't pass through the center, this theorem is indispensable. It states:
I = Icm + Md²
where:
Iis the moment of inertia about the new axisIcmis the moment of inertia about an axis through the center of mass (which we've already calculated)Mis the total mass of the shelldis the perpendicular distance between the two parallel axes.
Applications of Hollow Spherical Shell Moment of Inertia
Understanding the moment of inertia of a hollow spherical shell has numerous applications across various fields:
- Rotational Dynamics: Calculating angular acceleration, torque, and rotational kinetic energy in systems involving hollow spheres. Examples include gyroscopes, satellites, and rotating machinery.
- Mechanical Engineering: Designing and analyzing rotating components like flywheels, gears, and spherical bearings, ensuring efficient energy transfer and minimal stress.
- Aerospace Engineering: Modeling the rotational motion of satellites and spacecraft, crucial for maintaining stability and orientation.
- Physics Research: Investigating rotational phenomena at various scales, from atomic to astronomical, where spherical objects are common.
Comparison with Solid Sphere
It's instructive to compare the moment of inertia of a hollow spherical shell with that of a solid sphere of the same mass and radius. The moment of inertia of a solid sphere is (2/5)MR². Notice that the hollow sphere has a larger moment of inertia. This difference reflects the fact that the mass is distributed farther from the axis of rotation in the hollow sphere, making it more resistant to changes in rotational motion.
Advanced Considerations
This discussion has focused on a uniformly dense, perfectly spherical shell. In real-world scenarios, variations in density and imperfections in the shell's geometry can slightly alter the calculated moment of inertia. More advanced techniques, such as numerical integration or finite element analysis, might be necessary for more complex scenarios.
Conclusion
Calculating the moment of inertia of a hollow spherical shell is a fundamental problem with far-reaching implications. The derivation, explained in detail above, highlights the power of integral calculus in solving physics problems. Understanding this concept is critical for anyone working in fields involving rotational motion, from engineering design to fundamental physics research. By grasping the underlying principles and applying the parallel axis theorem, one can accurately determine the moment of inertia for various axes of rotation, enabling the precise analysis and modeling of dynamic systems. Remember, the formula (2/3)MR² is the cornerstone for understanding the rotational behavior of this ubiquitous shape.
Latest Posts
Latest Posts
-
Force Per Unit Area Is Termed
Mar 31, 2025
-
Consecutive Angles Of A Parallelogram Are Supplementary
Mar 31, 2025
-
What Are 5 Examples Of Chemical Weathering
Mar 31, 2025
-
5 Letter Words Starting With H A I
Mar 31, 2025
-
How Many Mm Are In One Meter
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Hollow Spherical Shell Moment Of Inertia . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
