What Is The Square Root Of 3600
Juapaving
Mar 29, 2025 · 5 min read
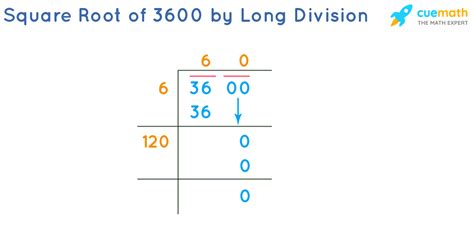
Table of Contents
What is the Square Root of 3600? A Deep Dive into Square Roots and Their Applications
The question, "What is the square root of 3600?" seems simple enough. A quick calculation reveals the answer: 60. But this seemingly straightforward mathematical problem opens a door to a fascinating world of mathematical concepts, their practical applications, and the history behind them. This article will not only answer the initial question but will also explore the broader topic of square roots, their properties, and their relevance in various fields.
Understanding Square Roots
Before delving into the specifics of the square root of 3600, let's establish a solid understanding of what a square root actually is. In simple terms, the square root of a number is a value that, when multiplied by itself (squared), gives the original number. For example, the square root of 9 is 3 because 3 x 3 = 9. Similarly, the square root of 16 is 4 because 4 x 4 = 16.
Mathematically, we represent the square root of a number 'x' as √x. Therefore, the question "What is the square root of 3600?" can be written as √3600.
Calculating the Square Root of 3600
There are several methods for calculating the square root of 3600:
1. Prime Factorization: This method is particularly useful for larger numbers. We break down 3600 into its prime factors:
3600 = 36 x 100 = (6 x 6) x (10 x 10) = (2 x 3) x (2 x 3) x (2 x 5) x (2 x 5) = 2⁴ x 3² x 5²
Since the square root involves finding pairs of identical factors, we can simplify:
√3600 = √(2⁴ x 3² x 5²) = 2² x 3 x 5 = 4 x 3 x 5 = 60
Therefore, the square root of 3600 is 60.
2. Using a Calculator: The simplest and often quickest method is to use a calculator. Most calculators have a dedicated square root function (√). Entering 3600 and pressing the square root button will instantly provide the answer: 60.
3. Long Division Method: While less common today due to the availability of calculators, the long division method for finding square roots is a useful manual technique, particularly for understanding the underlying principles. This method involves a series of iterative steps to progressively refine an approximation of the square root.
Properties of Square Roots
Understanding the properties of square roots is crucial for solving more complex mathematical problems. Some key properties include:
- √(a x b) = √a x √b: The square root of a product is equal to the product of the square roots.
- √(a / b) = √a / √b: The square root of a quotient is equal to the quotient of the square roots.
- (√a)² = a: Squaring the square root of a number returns the original number.
- √a² = |a|: The square root of a squared number is the absolute value of that number. This is important because the square root is always non-negative.
Applications of Square Roots in Real Life
Square roots aren't just abstract mathematical concepts; they have numerous practical applications across various fields:
1. Geometry and Measurement: Square roots are fundamental in calculating distances, areas, and volumes. For instance:
-
Pythagorean Theorem: This theorem, a cornerstone of geometry, uses square roots to find the length of the hypotenuse (the longest side) of a right-angled triangle: a² + b² = c², where 'c' is the hypotenuse. Finding 'c' requires taking the square root of (a² + b²). This is crucial in surveying, construction, and navigation.
-
Area Calculations: The area of a square is calculated as side², so finding the side length requires taking the square root of the area. Similarly, finding the radius of a circle from its area involves a square root calculation.
2. Physics and Engineering: Square roots appear frequently in physical formulas and engineering calculations:
-
Speed and Velocity: Calculating the speed or velocity often involves square roots, particularly in problems involving projectile motion or energy calculations.
-
Electrical Engineering: Calculations related to impedance, reactance, and power in AC circuits frequently involve square roots.
-
Mechanics: Analyzing forces, motion, and energy in mechanical systems often requires the use of square roots.
3. Statistics and Probability: Standard deviation, a key measure of data dispersion in statistics, involves calculating the square root of the variance. This helps determine the spread or variability of a dataset.
4. Computer Graphics and Game Development: Square roots are essential in many algorithms used in computer graphics and game development for tasks such as:
-
Calculating distances between points: This is vital for collision detection and pathfinding in games and simulations.
-
Transformations and rotations: Square roots are involved in matrix calculations for manipulating objects within a 3D space.
5. Finance and Investments: Square roots can be utilized in some financial calculations, particularly those involving standard deviation of returns in investment portfolio analysis. Understanding the risk and volatility of investments often relies on statistical measures that utilize square roots.
Exploring Further: Beyond the Square Root of 3600
While we have extensively covered the square root of 3600, this serves as a stepping stone to exploring more complex mathematical concepts. Consider the following expansions:
-
Cube roots: These are similar to square roots, but instead of finding a number that, when multiplied by itself, equals the original number, we look for a number that, when multiplied by itself three times, equals the original number (e.g., the cube root of 8 is 2 because 2 x 2 x 2 = 8).
-
Higher-order roots: The concept extends to fourth roots, fifth roots, and so on.
-
Complex numbers: The concept of square roots can be extended to include complex numbers, where we deal with numbers that involve the imaginary unit 'i' (defined as √-1).
Conclusion
The seemingly simple question, "What is the square root of 3600?" opens a wide-ranging discussion encompassing fundamental mathematical principles and their diverse applications in the real world. From the elegance of prime factorization to the practical applications in various fields, the concept of square roots is a testament to the power and versatility of mathematics. Understanding square roots is not only crucial for academic success but also for navigating and understanding the complexities of many aspects of our physical and digital world. The answer, 60, is just the beginning of a much larger and more interesting mathematical journey.
Latest Posts
Latest Posts
-
Is 2 3 Less Than 1 2
Apr 01, 2025
-
Is 23 A Prime Number Or Composite
Apr 01, 2025
-
Is The Square Root Of 45 A Rational Number
Apr 01, 2025
-
Which Phase Do Chromosomes First Become Visible
Apr 01, 2025
-
What Is The Least Common Multiple Of 3 And 2
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Is The Square Root Of 3600 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
