What Is The Relationship Between Length And Resistance
Juapaving
Apr 02, 2025 · 5 min read
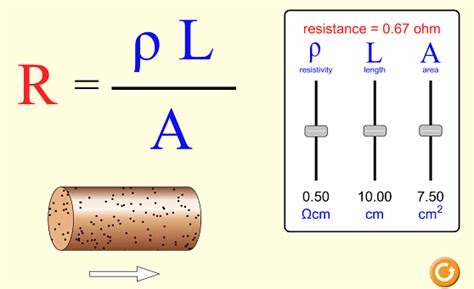
Table of Contents
The Relationship Between Length and Resistance: A Deep Dive
The relationship between the length of a conductor and its electrical resistance is a fundamental concept in physics and electrical engineering. Understanding this relationship is crucial for designing circuits, analyzing electrical systems, and predicting the behavior of materials under various conditions. This article delves deep into this relationship, exploring the underlying principles, the mathematical formula governing it, and its implications across diverse applications.
The Fundamental Principle: Resistance and Electron Flow
Electrical resistance is the opposition a material offers to the flow of electric current. At a microscopic level, this opposition arises from the interaction of moving electrons (charge carriers) with the atoms and molecules within the material. Longer conductors inherently present more obstacles to this electron flow. Imagine a river: a longer river will naturally offer more resistance to the flow of water than a shorter one, even if the cross-sectional area and the water's properties remain the same. Similarly, a longer wire impedes the movement of electrons more significantly.
Factors Affecting Resistance: Beyond Length
While length is a key factor, it's not the only one. The resistance (R) of a conductor is also influenced by its:
-
Cross-sectional area (A): A larger cross-sectional area provides more pathways for electrons to flow, reducing resistance. Think of wider roads allowing for smoother traffic flow. The relationship is inversely proportional: doubling the area halves the resistance.
-
Material resistivity (ρ): This intrinsic property reflects how easily electrons move through a specific material. Materials like copper have low resistivity (high conductivity), while materials like rubber have high resistivity (low conductivity). Resistivity is a constant for a given material at a specific temperature.
-
Temperature (T): Temperature affects the vibrational energy of atoms in the material. Increased vibrations disrupt electron flow, increasing resistance. This effect is usually positive; resistance increases with temperature for most conductors. However, some materials exhibit exceptions.
The Formula: Quantifying the Relationship
The relationship between length (L), cross-sectional area (A), resistivity (ρ), and resistance (R) is elegantly captured by the following formula:
R = ρL/A
This equation is a cornerstone of electrical engineering. Let's break down its significance:
-
Direct Proportionality with Length (L): The formula clearly shows a direct proportional relationship between resistance (R) and length (L). Doubling the length of a conductor doubles its resistance, assuming all other factors remain constant. This is because the electrons have to travel a longer distance, encountering more obstacles along the way.
-
Inverse Proportionality with Cross-sectional Area (A): Resistance (R) is inversely proportional to the cross-sectional area (A). Doubling the cross-sectional area halves the resistance. This is because a larger area provides more space for electrons to flow, reducing the overall resistance to the flow of current.
-
Dependence on Material Resistivity (ρ): The material's resistivity (ρ) is a crucial factor. Materials with lower resistivity offer less resistance to current flow. Copper's low resistivity makes it a popular choice for wiring, while materials with high resistivity are often used as insulators.
Applications and Implications
The relationship between length and resistance has wide-ranging applications across various fields:
1. Electrical Wiring Design
The length of wires significantly impacts the overall resistance of a circuit. Longer wires lead to increased voltage drops, potentially impacting the performance of connected devices. Engineers carefully select wire gauges (which determine the cross-sectional area) and materials to minimize resistance and ensure efficient power delivery over the required lengths. In long-distance power transmission, minimizing resistance is crucial to reduce energy loss.
2. Resistor Manufacturing
Resistors are essential components in electronic circuits, used to control current flow. Their resistance is precisely controlled during manufacturing by adjusting the length, cross-sectional area, and material of the resistive element. By precisely controlling these parameters, manufacturers can produce resistors with specific resistance values.
3. Sensing Applications
The change in resistance with length forms the basis of several sensing applications. For example, strain gauges utilize this principle. A strain gauge is a resistor whose resistance changes when subjected to mechanical stress. The change in resistance is directly related to the strain (elongation or compression), enabling the measurement of force, pressure, or displacement.
4. Temperature Measurement
The dependence of resistance on temperature (thermistors) is used in temperature sensing. As temperature changes, the resistance of a thermistor changes predictably. By measuring the resistance, the temperature can be accurately determined. This is widely used in various applications, from automotive systems to medical devices.
5. Material Characterization
The relationship between length, area, and resistance provides a method to determine the resistivity of unknown materials. By measuring the resistance of a known length and cross-sectional area, the material's resistivity can be calculated, providing valuable information about its electrical properties. This is vital in material science research and development.
Beyond the Ideal: Real-World Considerations
The formula R = ρL/A provides an idealized model. In real-world scenarios, several factors can deviate from this ideal:
-
Non-uniform cross-section: If the conductor's cross-sectional area is not uniform along its length, the resistance calculation becomes more complex. Numerical methods or approximations are often necessary.
-
Temperature variations: Temperature is not always uniform throughout the conductor. Temperature gradients can lead to non-uniform resistance distributions.
-
Skin effect: At high frequencies, current tends to flow mostly on the surface of the conductor (skin effect), effectively reducing the usable cross-sectional area and increasing resistance.
-
Proximity effect: The presence of other conductors nearby can influence the distribution of current and affect the overall resistance.
Conclusion: A Cornerstone of Electrical Engineering
The relationship between length and resistance is a cornerstone principle in electrical engineering and physics. The simple yet powerful formula R = ρL/A provides a fundamental understanding of how conductor geometry and material properties influence resistance. Understanding this relationship is crucial for designing efficient circuits, developing advanced sensors, and characterizing materials. While real-world scenarios often present complexities beyond this basic model, the foundational principle remains essential for analyzing and predicting the behavior of electrical systems. This knowledge is critical across various engineering disciplines and contributes significantly to technological advancements.
Latest Posts
Latest Posts
-
The Pectoral Girdle Consists Of The
Apr 03, 2025
-
Find The Unit Vector In The Direction Of V
Apr 03, 2025
-
5 Letter Words Starting With Ho
Apr 03, 2025
-
Partial Fraction Decomposition Calculator Step By Step
Apr 03, 2025
-
5 Letter Words Starting With Har
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about What Is The Relationship Between Length And Resistance . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
