Find The Unit Vector In The Direction Of V
Juapaving
Apr 03, 2025 · 5 min read
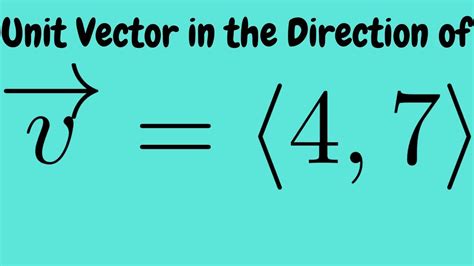
Table of Contents
Finding the Unit Vector in the Direction of v: A Comprehensive Guide
Finding the unit vector in the direction of a given vector v is a fundamental concept in linear algebra and vector calculus with widespread applications in physics, computer graphics, and machine learning. This comprehensive guide will explore the process in detail, covering various aspects and providing practical examples to solidify your understanding.
Understanding Vectors and Unit Vectors
Before diving into the calculation, let's clarify the core concepts:
-
Vector: A vector is a mathematical object that has both magnitude (length) and direction. It's often represented as an arrow, where the length corresponds to the magnitude and the arrowhead indicates the direction. We can represent vectors using coordinates, like v = (v<sub>x</sub>, v<sub>y</sub>, v<sub>z</sub>) in three-dimensional space.
-
Magnitude (Length) of a Vector: The magnitude of a vector v, often denoted as ||v|| or |v|, represents its length. For a vector in three dimensions, the magnitude is calculated using the Pythagorean theorem in three dimensions: ||v|| = √(v<sub>x</sub>² + v<sub>y</sub>² + v<sub>z</sub>²).
-
Unit Vector: A unit vector is a vector with a magnitude of exactly 1. It's essentially a direction indicator; it tells us the direction but doesn't provide information about the length. Unit vectors are crucial for representing directions without the complication of varying magnitudes.
Calculating the Unit Vector
The process of finding the unit vector in the direction of a vector v is straightforward: you simply divide the vector by its magnitude. This scales the vector down to a length of 1 while maintaining its original direction. Mathematically:
û = v / ||v||
where:
- û represents the unit vector.
- v is the original vector.
- ||v|| is the magnitude of the vector v.
This formula applies to vectors in any number of dimensions (2D, 3D, or higher).
Step-by-Step Procedure
Let's break down the process into clear steps:
-
Find the Magnitude: Calculate the magnitude of the vector v using the formula mentioned earlier. Remember to square each component, sum the squares, and then take the square root.
-
Divide the Vector by its Magnitude: Divide each component of the vector v by the magnitude calculated in step 1. This creates a new vector where each component is scaled down proportionally.
-
Verify the Magnitude: As a final check, calculate the magnitude of the resulting unit vector. It should be very close to 1 (minor discrepancies might arise due to rounding errors in calculations).
Examples in Different Dimensions
Let's illustrate the process with examples in 2D and 3D spaces.
Example 1: 2D Vector
Let's say we have a 2D vector v = (3, 4).
-
Magnitude: ||v|| = √(3² + 4²) = √(9 + 16) = √25 = 5
-
Unit Vector: û = (3/5, 4/5)
-
Verification: ||û|| = √((3/5)² + (4/5)²) = √(9/25 + 16/25) = √(25/25) = 1
Example 2: 3D Vector
Consider a 3D vector v = (1, 2, 2).
-
Magnitude: ||v|| = √(1² + 2² + 2²) = √(1 + 4 + 4) = √9 = 3
-
Unit Vector: û = (1/3, 2/3, 2/3)
-
Verification: ||û|| = √((1/3)² + (2/3)² + (2/3)²) = √(1/9 + 4/9 + 4/9) = √(9/9) = 1
Applications of Unit Vectors
Unit vectors are ubiquitous in various fields:
1. Physics
- Direction of Force: Representing the direction of a force vector.
- Velocity and Acceleration: Indicating the direction of velocity and acceleration vectors.
- Normalization of Vectors: Normalizing vectors to a unit length ensures that only the direction matters in calculations, eliminating the effect of the vector's magnitude.
2. Computer Graphics
- Lighting Calculations: In computer graphics, unit vectors are essential for lighting calculations, determining the direction of light sources.
- 3D Modeling and Animation: They play a critical role in defining surface normals, which influence how surfaces interact with light and shadows.
- Camera Orientation: Defining camera orientation and viewpoint in 3D scenes.
3. Machine Learning
- Normalization of Data: Normalizing feature vectors to unit length in machine learning algorithms like Support Vector Machines (SVMs) can improve performance.
- Dimensionality Reduction: Used in techniques like Principal Component Analysis (PCA) to represent data in a lower-dimensional space while preserving important information.
Handling the Zero Vector
A special case arises when dealing with the zero vector (v = (0, 0, 0) or equivalent in other dimensions). The magnitude of the zero vector is 0. Dividing by 0 is undefined, so the unit vector for the zero vector is not defined.
Advanced Concepts and Considerations
While the basic calculation is straightforward, more complex scenarios can arise:
-
Vectors in Higher Dimensions: The process remains the same regardless of the number of dimensions. You simply extend the magnitude calculation and component-wise division to accommodate more components.
-
Numerical Stability: When dealing with very small magnitudes, there's a potential for numerical instability. Be mindful of potential rounding errors and consider using higher-precision arithmetic if necessary.
-
Programming Implementation: Implementing the unit vector calculation in programming languages (Python, MATLAB, C++, etc.) is straightforward, often utilizing built-in vector libraries for efficiency and convenience.
Conclusion
Finding the unit vector in the direction of a given vector is a core concept with broad applications. Understanding the calculation, its implications, and its applications is fundamental for anyone working with vectors and linear algebra. By following the step-by-step procedure outlined above and understanding the underlying principles, you can confidently perform this essential calculation and utilize unit vectors effectively in various contexts. Remember to always consider potential numerical issues, especially when dealing with vectors of small magnitudes or in higher dimensions. The versatility and importance of unit vectors in various domains make mastering this concept a valuable asset in any technical field.
Latest Posts
Latest Posts
-
As Temperature Increases The Rate Of Diffusion
Apr 03, 2025
-
Is 87 Prime Or Composite Number
Apr 03, 2025
-
Least Common Multiple 15 And 25
Apr 03, 2025
-
How Many Electrons Can Occupy The 3d Subshell
Apr 03, 2025
-
Difference Between And Enzyme And A Hormone
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Find The Unit Vector In The Direction Of V . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
