What Is The Rate At Which Velocity Changes
Juapaving
Apr 06, 2025 · 6 min read
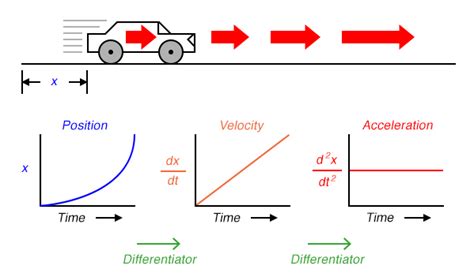
Table of Contents
What is the Rate at Which Velocity Changes?
The rate at which velocity changes is known as acceleration. Understanding acceleration is crucial in physics, engineering, and numerous other fields, as it describes the dynamism of motion. This comprehensive guide will delve into the multifaceted nature of acceleration, exploring its definition, types, calculations, and real-world applications.
Understanding Acceleration: Beyond Just Speeding Up
Many associate acceleration solely with an increase in speed. While this is a common scenario, acceleration encompasses more than just speeding up. It's a vector quantity, meaning it has both magnitude (size or amount) and direction. Therefore, a change in either speed or direction, or both, constitutes acceleration.
Key Aspects of Acceleration:
-
Change in Velocity: The fundamental aspect of acceleration is a change in velocity. Velocity, unlike speed, considers both the rate of movement and the direction of travel. A car traveling at a constant 60 mph in a straight line has zero acceleration. However, if it speeds up, slows down, or turns, it experiences acceleration.
-
Magnitude and Direction: Acceleration is a vector, so it possesses both magnitude (measured in meters per second squared (m/s²) or feet per second squared (ft/s²)) and direction. A positive acceleration indicates an increase in velocity, while a negative acceleration (also called deceleration or retardation) indicates a decrease in velocity.
-
Instantaneous vs. Average Acceleration: Instantaneous acceleration refers to the acceleration at a specific moment in time. Average acceleration, on the other hand, represents the overall change in velocity over a given time interval.
Types of Acceleration: Exploring the Nuances
The concept of acceleration encompasses various types, each with unique characteristics:
1. Uniform Acceleration: The Steady Pace
Uniform acceleration, also known as constant acceleration, occurs when the velocity changes at a consistent rate. This means the acceleration vector remains constant in both magnitude and direction. A classic example is a freely falling object under the influence of gravity (neglecting air resistance), experiencing a nearly constant downward acceleration of approximately 9.8 m/s².
2. Non-Uniform Acceleration: The Dynamic Shift
Non-uniform acceleration describes scenarios where the rate of change in velocity is not constant. This is the most common type of acceleration encountered in real-world situations. A car accelerating from a standstill, for instance, experiences non-uniform acceleration as the driver gradually increases the throttle. The acceleration changes constantly as the car's speed increases.
3. Centripetal Acceleration: The Circular Motion
Centripetal acceleration arises when an object moves in a circular path at a constant speed. Although the speed remains unchanged, the direction of velocity is constantly changing, resulting in acceleration directed towards the center of the circle. This acceleration is responsible for keeping the object moving along the curved path. Think of a car rounding a bend—it's constantly accelerating toward the center of the turn.
4. Tangential Acceleration: The Speed Shift in Circular Motion
Tangential acceleration, in contrast to centripetal acceleration, is the component of acceleration that is tangent to the circular path. It represents the change in the speed of an object moving in a circle. A car speeding up while going around a curve experiences both tangential and centripetal acceleration.
Calculating Acceleration: The Mathematical Perspective
The calculation of acceleration depends on the available information. Here are some key formulas:
1. Average Acceleration: The Overall Change
The formula for average acceleration is:
a = (v_f - v_i) / t
Where:
- a represents average acceleration
- v_f represents the final velocity
- v_i represents the initial velocity
- t represents the time interval
2. Instantaneous Acceleration: The Momentary Change
Calculating instantaneous acceleration requires calculus and involves finding the derivative of the velocity function with respect to time. This gives the acceleration at any specific point in time. For example, if the velocity function is v(t) = 2t² + 3t, then the instantaneous acceleration is a(t) = 4t + 3.
3. Acceleration Due to Gravity: The Earth's Pull
The acceleration due to gravity (g) is approximately 9.8 m/s² on the Earth's surface. This value is used in many physics problems involving falling objects or projectiles.
Real-World Applications: Acceleration in Action
Acceleration's influence extends far beyond theoretical physics. It plays a crucial role in various real-world applications:
1. Automotive Engineering: Designing for Performance and Safety
The automotive industry heavily relies on an understanding of acceleration to design vehicles with optimal performance and safety features. Engineers meticulously analyze acceleration curves to optimize engine performance, braking systems, and overall vehicle handling. Anti-lock braking systems (ABS), for example, use controlled acceleration and deceleration to prevent wheel lockup during braking.
2. Aerospace Engineering: Launching Rockets and Controlling Flight
Rocket propulsion relies fundamentally on acceleration. The powerful thrust generated by rocket engines produces immense acceleration, propelling spacecraft into orbit or beyond. Aerospace engineers utilize intricate calculations of acceleration to design flight control systems, enabling precise maneuvers and safe landings.
3. Sports Science: Enhancing Athletic Performance
In sports science, the analysis of acceleration helps athletes improve their performance. Coaches and trainers use sophisticated instruments to measure an athlete's acceleration during various activities, providing insights into training regimens and technique adjustments. For example, sprint coaches might analyze a runner's acceleration to optimize their starting technique and stride length.
4. Robotics: Programming Precise Movements
The programming of robots often involves meticulous calculations of acceleration to ensure precise movements and avoid collisions. Industrial robots, for example, require precise control of acceleration to handle delicate objects or perform complex tasks.
5. Physics Experiments: Unveiling Nature's Secrets
Numerous physics experiments rely on measuring and controlling acceleration to unveil fundamental principles of motion and mechanics. Experiments involving projectiles, pendulums, and inclined planes all rely on a deep understanding of acceleration and its relationship to other physical quantities such as force and mass.
Beyond the Basics: Exploring Advanced Concepts
The exploration of acceleration extends beyond the fundamental concepts discussed above. Advanced physics delves into more complex scenarios, such as:
-
Relativistic Acceleration: At very high speeds, approaching the speed of light, classical mechanics breaks down, and relativistic mechanics must be employed to accurately describe acceleration.
-
Non-linear Acceleration: In many real-world systems, acceleration is not a simple linear function of time. Understanding these complex relationships often requires advanced mathematical tools and numerical methods.
-
Acceleration in Multiple Dimensions: The concept of acceleration can be extended to three-dimensional space, requiring vector calculus for accurate representation and calculations.
-
The Relationship between Acceleration, Force, and Mass: Newton's second law of motion (F = ma) establishes the fundamental relationship between force, mass, and acceleration, providing a cornerstone for understanding the dynamics of moving objects.
Conclusion: A Cornerstone of Physics and Beyond
Understanding the rate at which velocity changes—acceleration—is a cornerstone of physics and its applications across numerous fields. From designing high-performance vehicles to programming robots, the ability to calculate, analyze, and control acceleration is essential. This comprehensive guide has explored the fundamental aspects of acceleration, including its various types, calculation methods, and real-world applications, equipping readers with a solid foundation to further explore this critical concept in physics and engineering. The constant evolution of technology and scientific understanding will continue to unveil new and more complex applications for the principle of acceleration, underscoring its continued relevance in scientific advancement.
Latest Posts
Latest Posts
-
How Do You Find The Perimeter Of A Right Triangle
Apr 07, 2025
-
How Many Feet Is 92 In
Apr 07, 2025
-
Is Sound Kinetic Or Potential Energy
Apr 07, 2025
-
Lcm Of 3 4 And 7
Apr 07, 2025
-
What Is Another Way To Get 19
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about What Is The Rate At Which Velocity Changes . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
