How Do You Find The Perimeter Of A Right Triangle
Juapaving
Apr 07, 2025 · 5 min read
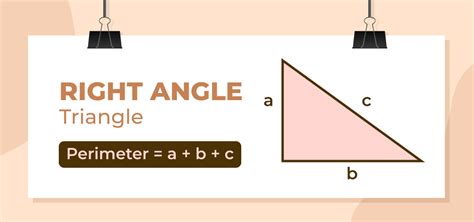
Table of Contents
How Do You Find the Perimeter of a Right Triangle? A Comprehensive Guide
Finding the perimeter of any shape, including a right triangle, is a fundamental concept in geometry. Understanding how to calculate this perimeter is crucial for various applications, from basic construction to advanced engineering projects. This comprehensive guide will walk you through different methods to determine the perimeter of a right triangle, catering to various levels of mathematical understanding. We'll cover the basics, explore different scenarios, and even delve into some problem-solving strategies.
Understanding the Basics: Perimeter and Right Triangles
Before diving into the calculations, let's clarify some key terms.
Perimeter: The perimeter of any polygon (a shape with straight sides) is the total distance around its exterior. Think of it as the length of a continuous line tracing the outline of the shape. For a triangle, it's simply the sum of the lengths of its three sides.
Right Triangle: A right triangle is a specific type of triangle characterized by one 90-degree angle (a right angle). This right angle is often marked with a small square in diagrams. The side opposite the right angle is called the hypotenuse, and the other two sides are called legs or cathetus.
Method 1: Knowing All Three Sides
The simplest method to find the perimeter of a right triangle is when you already know the lengths of all three sides. This is a straightforward addition problem.
Formula: Perimeter = Side a + Side b + Hypotenuse (c)
Example:
Let's say we have a right triangle with sides a = 3 cm, b = 4 cm, and hypotenuse c = 5 cm.
Perimeter = 3 cm + 4 cm + 5 cm = 12 cm
Therefore, the perimeter of this right triangle is 12 centimeters.
Method 2: Using the Pythagorean Theorem When Two Sides are Known
Often, you might only know the lengths of two sides of a right triangle. This is where the Pythagorean Theorem comes into play. This theorem is a cornerstone of geometry and states:
Pythagorean Theorem: a² + b² = c²
where:
- a and b are the lengths of the two legs (cathetus) of the right triangle.
- c is the length of the hypotenuse.
This theorem allows you to calculate the length of the unknown side (either a leg or the hypotenuse) if you know the lengths of the other two. Once you have all three side lengths, you can calculate the perimeter using the method described above.
Example 1: Finding the Hypotenuse
Suppose you know the lengths of the two legs: a = 6 inches and b = 8 inches. You need to find the hypotenuse (c) before calculating the perimeter.
- Apply the Pythagorean Theorem: 6² + 8² = c²
- Solve for c: 36 + 64 = c² => 100 = c² => c = √100 = 10 inches
- Calculate the perimeter: Perimeter = 6 inches + 8 inches + 10 inches = 24 inches
Example 2: Finding a Leg
Let's say you know the hypotenuse (c = 13 meters) and one leg (a = 5 meters). You need to find the other leg (b) before calculating the perimeter.
- Apply the Pythagorean Theorem: 5² + b² = 13²
- Solve for b: 25 + b² = 169 => b² = 169 - 25 = 144 => b = √144 = 12 meters
- Calculate the perimeter: Perimeter = 5 meters + 12 meters + 13 meters = 30 meters
Method 3: Using Trigonometry When One Side and One Angle are Known
Trigonometry provides another powerful tool for finding the perimeter of a right triangle, especially when you know one side and one of the acute angles (angles other than the right angle).
The key trigonometric functions are:
- Sine (sin): sin(θ) = opposite side / hypotenuse
- Cosine (cos): cos(θ) = adjacent side / hypotenuse
- Tangent (tan): tan(θ) = opposite side / adjacent side
Where θ (theta) represents the acute angle.
Example:
Let's assume you know one leg (a = 7 cm) and one acute angle (θ = 30°). We can use trigonometric functions to find the other sides and then the perimeter.
- Find the hypotenuse (c): We can use cosine since we know the adjacent side (a) and the angle (θ). cos(30°) = 7 cm / c c = 7 cm / cos(30°) (Remember to use a calculator to find the value of cos(30°))
- Find the other leg (b): We can use tangent since we know one leg (a) and the angle (θ). tan(30°) = b / 7 cm b = 7 cm * tan(30°)
- Calculate the perimeter: Perimeter = a + b + c
Remember to always use a calculator with trigonometric functions to find the accurate values of sin, cos, and tan for the given angle.
Solving Real-World Problems
The ability to calculate the perimeter of a right triangle isn't just an academic exercise; it has numerous practical applications:
- Construction: Determining the amount of fencing needed for a triangular plot of land.
- Engineering: Calculating the length of bracing materials for structural support.
- Navigation: Determining distances using triangulation techniques.
- Cartography: Measuring distances on maps representing right-angled areas.
- Computer Graphics: Creating accurate representations of triangular shapes in 3D modeling.
Advanced Concepts and Considerations
Significant Figures and Accuracy: When dealing with real-world measurements, remember to pay attention to significant figures. Your final answer should reflect the accuracy of your initial measurements.
Units of Measurement: Always maintain consistency in units throughout your calculations. If your side lengths are in meters, your perimeter will also be in meters.
Special Right Triangles: Some right triangles have special properties that simplify calculations. These include:
- 45-45-90 triangles (Isosceles Right Triangles): The two legs are equal in length.
- 30-60-90 triangles: The sides have a specific ratio (1:√3:2).
Knowing these properties can speed up calculations.
Approximations: When dealing with irrational numbers (like √2 or √3), you might need to round your answers to a specific number of decimal places.
Practice Problems
To solidify your understanding, try these practice problems:
- A right triangle has legs of length 9 cm and 12 cm. Find its perimeter.
- A right triangle has a hypotenuse of 15 inches and one leg of 9 inches. Find its perimeter.
- A right triangle has a hypotenuse of 10 feet and one acute angle of 45°. Find its perimeter.
By working through these examples and problems, you'll gain confidence in calculating the perimeter of a right triangle using various methods. Remember to always double-check your calculations and consider the context of the problem to ensure accurate results. The ability to calculate the perimeter efficiently is a valuable skill in numerous fields.
Latest Posts
Latest Posts
-
Which Is The Most Abundant Gas In Earths Atmosphere
Apr 07, 2025
-
What Is The Molar Mass Of Chcl3
Apr 07, 2025
-
How Many Neutrons Are In Argon
Apr 07, 2025
-
Does Acid Turn Litmus Paper Red
Apr 07, 2025
-
Is Sno2 A Solid Or Gas
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about How Do You Find The Perimeter Of A Right Triangle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.