Lcm Of 3 4 And 7
Juapaving
Apr 07, 2025 · 5 min read
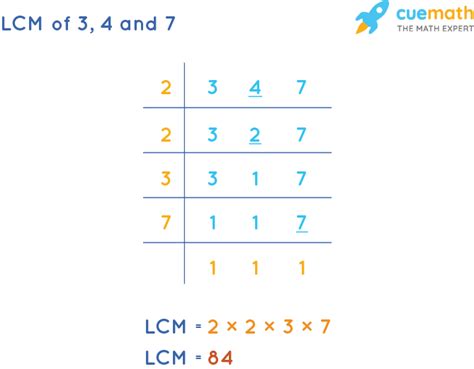
Table of Contents
Finding the Least Common Multiple (LCM) of 3, 4, and 7: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics with wide-ranging applications. Understanding how to calculate the LCM is crucial for various mathematical operations, from simplifying fractions to solving complex equations. This article will delve into the process of finding the LCM of 3, 4, and 7, exploring various methods and providing a comprehensive understanding of the underlying principles. We'll also touch upon the significance of LCM in real-world scenarios and its connection to other mathematical concepts like the greatest common divisor (GCD).
Understanding Least Common Multiple (LCM)
Before we embark on calculating the LCM of 3, 4, and 7, let's solidify our understanding of the concept. The LCM of a set of numbers is the smallest positive integer that is a multiple of all the numbers in the set. In simpler terms, it's the smallest number that all the numbers in the set can divide into evenly. For instance, the LCM of 2 and 3 is 6 because 6 is the smallest number divisible by both 2 and 3.
Key Characteristics of LCM:
- Positive Integer: The LCM is always a positive whole number.
- Smallest Multiple: It's the smallest number that satisfies the divisibility condition for all the numbers in the set.
- Multiple of all numbers: The LCM is a multiple of each number in the given set.
Methods for Calculating LCM
Several methods exist for calculating the LCM of a set of numbers. We'll explore two common approaches: the listing method and the prime factorization method. Both methods are effective, but the prime factorization method is generally more efficient for larger numbers or a greater number of integers.
1. Listing Method
This method involves listing the multiples of each number until we find the smallest common multiple. While straightforward for smaller numbers, it becomes cumbersome for larger numbers or a larger set of integers.
Let's apply this method to find the LCM of 3, 4, and 7:
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84...
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, 80, 84...
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84...
By examining the lists, we can see that the smallest number common to all three lists is 84. Therefore, the LCM of 3, 4, and 7 is 84.
2. Prime Factorization Method
This method is generally more efficient, especially when dealing with larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of all prime factors present.
Let's use this method to find the LCM of 3, 4, and 7:
-
Prime Factorization:
- 3 = 3
- 4 = 2²
- 7 = 7
-
Identify the highest powers of each prime factor:
- The prime factors are 2, 3, and 7.
- The highest power of 2 is 2².
- The highest power of 3 is 3.
- The highest power of 7 is 7.
-
Calculate the LCM:
- LCM(3, 4, 7) = 2² × 3 × 7 = 4 × 3 × 7 = 84
Therefore, the LCM of 3, 4, and 7 is 84, confirming the result obtained using the listing method.
Applications of LCM
The LCM finds practical application in various areas, including:
-
Fraction Addition and Subtraction: Finding a common denominator when adding or subtracting fractions often involves determining the LCM of the denominators. For example, to add 1/3 and 1/4, we need to find the LCM of 3 and 4, which is 12. We then rewrite the fractions with a common denominator of 12 before adding them.
-
Scheduling Problems: LCM is useful in solving scheduling problems. For instance, if Event A occurs every 3 days, Event B every 4 days, and Event C every 7 days, the LCM (84) represents the number of days after which all three events will occur on the same day again.
-
Modular Arithmetic: The LCM plays a significant role in modular arithmetic, a branch of number theory that deals with remainders after division.
-
Music Theory: LCM helps in understanding rhythmic patterns and finding the least common denominator for musical time signatures.
-
Engineering and Design: In various engineering applications, determining common cycles or frequencies often requires calculating the LCM.
Relationship Between LCM and GCD
The least common multiple (LCM) and the greatest common divisor (GCD) are closely related concepts. For any two integers a and b, the product of their LCM and GCD is equal to the product of the two numbers:
LCM(a, b) × GCD(a, b) = a × b
This relationship provides an alternative method for calculating the LCM if the GCD is known. For our example (3, 4, 7), the GCD is 1 (as 3, 4, and 7 are coprime - they share no common factors other than 1). Therefore, using this relationship would still lead to LCM(3,4,7) = (347)/GCD(3,4,7) = 84/1 = 84.
Advanced Techniques for Larger Sets of Numbers
For larger sets of numbers or significantly larger numbers, utilizing a combination of the prime factorization method and efficient algorithms becomes advantageous. Computer programs and mathematical software are often employed to handle these complex calculations effectively.
Conclusion
Calculating the least common multiple is a fundamental mathematical skill with practical applications in various fields. The methods outlined in this article – the listing method and the prime factorization method – provide effective strategies for determining the LCM, particularly for smaller sets of numbers. The prime factorization method offers significant advantages in efficiency when dealing with larger numbers or a greater number of integers. Understanding the connection between LCM and GCD further enhances our ability to solve mathematical problems and analyze numerical relationships. Mastering the LCM concept provides a robust foundation for tackling more complex mathematical challenges and applying these principles to solve real-world problems across various disciplines.
Latest Posts
Latest Posts
-
How Many Neutrons Are In Argon
Apr 07, 2025
-
Does Acid Turn Litmus Paper Red
Apr 07, 2025
-
Is Sno2 A Solid Or Gas
Apr 07, 2025
-
Is 15 By 15 Bigger Than 16 By 10
Apr 07, 2025
-
112 Inches Is How Many Feet
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 3 4 And 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.