What Is The Probability Of An Impossible Event
Juapaving
Mar 27, 2025 · 5 min read
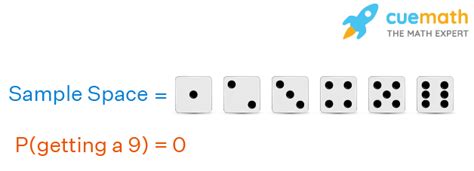
Table of Contents
What is the Probability of an Impossible Event?
The probability of an impossible event is a fundamental concept in probability theory, statistics, and related fields. Understanding this concept is crucial for building a solid foundation in these areas. This article delves into the intricacies of this seemingly simple yet important idea, exploring its definition, implications, and applications across various contexts.
Defining Impossible Events
An impossible event is an event that cannot occur under any circumstances. It's an event that has zero chance of happening. This differs from events with a very low probability, which still possess a theoretical possibility of occurring, however small. An impossible event, on the other hand, is categorically excluded from the set of possible outcomes.
Consider these examples:
- Rolling a 7 on a standard six-sided die: A standard die only has faces numbered 1 through 6. Rolling a 7 is impossible.
- Finding a red ball in a bag containing only blue balls: If the bag contains exclusively blue balls, finding a red one is impossible.
- A person being both 25 years old and 30 years old simultaneously: This violates the basic principles of time and age. It's an impossible event.
- The sun rising in the west: Based on our current understanding of celestial mechanics, this event is impossible.
Probability and the Impossible Event
The probability of any event is a numerical value between 0 and 1, inclusive. 0 represents an impossible event, while 1 represents a certain event. Any value between 0 and 1 indicates varying degrees of likelihood. Therefore, the probability of an impossible event is definitively 0.
This is represented mathematically as:
P(Impossible Event) = 0
Where P denotes probability. This is a foundational axiom of probability theory. No matter how you approach the calculation, the probability of an impossible event will always yield zero.
Distinguishing Between Impossible and Unlikely Events
It's crucial to differentiate between impossible and highly unlikely events. An unlikely event, while having a low probability, still has a theoretical chance of occurring. The probability is close to 0 but not exactly 0.
For example:
- Winning the lottery: The probability of winning a major lottery is incredibly low, but it's not zero. Someone could win; it's just highly improbable.
- Being struck by lightning: This is a low-probability event, but it does happen. Therefore, it's not impossible.
- Flipping heads 100 times in a row: While incredibly unlikely, it’s theoretically possible.
Applications of the Concept of Impossible Events
The concept of impossible events plays a critical role in various applications:
- Formal Logic and Set Theory: In logic and set theory, impossible events correspond to the empty set – a set containing no elements. Understanding this connection is essential for mathematical reasoning.
- Statistical Modeling: Statistical models often incorporate the possibility of impossible events, particularly in defining the boundaries of the model's validity.
- Risk Assessment: Identifying impossible events is a vital part of risk assessment. By excluding impossible scenarios, analysts can focus on realistic threats and vulnerabilities.
- Decision Making under Uncertainty: Recognizing impossible events helps to refine decision-making processes by eliminating irrelevant possibilities, leading to more efficient and effective choices.
- Computer Programming and Algorithm Design: In programming, handling impossible events often involves error checking and exception handling to ensure the robustness of software systems. Recognizing impossible states allows for the design of more efficient and reliable algorithms.
- Game Theory: In game theory, the understanding of impossible outcomes helps in streamlining the analysis of strategic interactions and predicting the outcomes of different scenarios.
Complement and Impossible Events
In probability theory, the complement of an event A, denoted as A', represents all outcomes that are not in A. If A is an impossible event (P(A) = 0), then its complement A' is a certain event (P(A') = 1). This relationship is a direct consequence of the fact that the sum of the probabilities of an event and its complement must always equal 1.
Therefore, if P(A) = 0, then P(A') = 1 - P(A) = 1 - 0 = 1.
Conditional Probability and Impossible Events
Conditional probability deals with the probability of an event given that another event has already occurred. If the conditioning event is impossible, the conditional probability is undefined. This is because you cannot have a probability based on an event that cannot happen.
For instance, let's say event A is "drawing a red ball from a bag of only blue balls", and event B is "drawing a blue ball from the same bag". Event A is impossible. The conditional probability P(B|A) – the probability of drawing a blue ball given that a red ball was already drawn – is undefined because event A is impossible.
Misinterpretations and Common Errors
A common misunderstanding is confusing an extremely low probability with an impossible event. Just because an event is highly unlikely doesn't mean it's impossible. This is crucial when evaluating risks and making decisions based on probability. Carefully considering the difference between unlikely and impossible is essential for accurate assessments.
Advanced Concepts and Extensions
The concept of impossible events extends to more advanced areas of probability and statistics, such as:
- Measure Theory: In measure theory, the probability measure assigns a measure of 0 to impossible events.
- Bayesian Statistics: Bayesian methods incorporate prior probabilities, which can reflect beliefs about the possibility or impossibility of certain events.
- Stochastic Processes: Stochastic processes can involve the modeling of events that are initially possible but may become impossible based on subsequent events in the process.
Conclusion
The probability of an impossible event is unequivocally 0. This seemingly simple concept is a cornerstone of probability theory, impacting various fields. Understanding the distinction between impossible and highly unlikely events is vital for accurate analysis, informed decision-making, and building robust models. By grasping this fundamental concept and its applications, one can develop a stronger foundation in probability, statistics, and related disciplines. The ability to correctly identify and handle impossible events is key to successful problem-solving and achieving accurate predictions in many areas of science, engineering, and everyday life.
Latest Posts
Latest Posts
-
A Body Of Land Surrounded By Water On Three Sides
Mar 30, 2025
-
Is Square Root Of 15 An Irrational Number
Mar 30, 2025
-
When The Owner Withdraws Cash For Personal Use
Mar 30, 2025
-
What Is The Hybridization Of The Central Atom In Sf4
Mar 30, 2025
-
Model Of A Animal Cell With Labels
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about What Is The Probability Of An Impossible Event . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
