What Is The Prime Factorization Of 420
Juapaving
Mar 31, 2025 · 5 min read
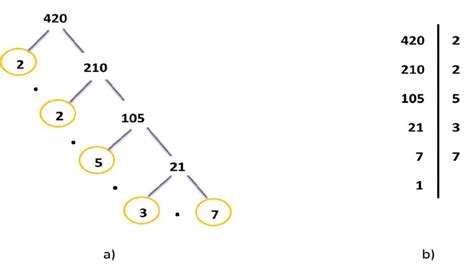
Table of Contents
- What Is The Prime Factorization Of 420
- Table of Contents
- What is the Prime Factorization of 420? A Deep Dive into Prime Numbers and Factorization
- Understanding Prime Numbers
- Identifying Prime Numbers
- The Importance of Prime Numbers
- Prime Factorization: Breaking Down Numbers
- The Process of Prime Factorization
- Finding the Prime Factorization of 420
- Applications of Prime Factorization
- Advanced Techniques for Prime Factorization
- Conclusion: The Enduring Significance of Prime Factorization
- Latest Posts
- Latest Posts
- Related Post
What is the Prime Factorization of 420? A Deep Dive into Prime Numbers and Factorization
The seemingly simple question, "What is the prime factorization of 420?" opens a door to a fascinating world of number theory. While the answer itself is relatively straightforward, understanding the process and the underlying concepts of prime numbers and factorization is crucial for anyone interested in mathematics, computer science, or cryptography. This article will not only provide the answer but also delve into the "why" and "how" behind prime factorization, exploring its significance and applications.
Understanding Prime Numbers
Before tackling the prime factorization of 420, let's establish a firm grasp on the definition of a prime number. A prime number is a natural number greater than 1 that is not a product of two smaller natural numbers. In simpler terms, it's only divisible by 1 and itself. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on. These numbers form the building blocks of all other natural numbers.
Identifying Prime Numbers
Determining whether a number is prime can be surprisingly complex for larger numbers. While simple divisibility tests exist for small numbers, sophisticated algorithms are employed for larger ones to check for primality efficiently. The Sieve of Eratosthenes is a classic algorithm used to identify prime numbers within a given range.
The Importance of Prime Numbers
Prime numbers are far from just mathematical curiosities. They are fundamental to various fields:
- Cryptography: The security of many encryption algorithms, including RSA, relies heavily on the difficulty of factoring large numbers into their prime components. The larger the prime numbers used, the more secure the encryption.
- Computer Science: Prime numbers are used in hash table algorithms, data structure optimization, and random number generation.
- Number Theory: Prime numbers are the cornerstone of many fundamental theorems and conjectures in number theory, such as the Riemann Hypothesis, which remains one of the most significant unsolved problems in mathematics.
Prime Factorization: Breaking Down Numbers
Prime factorization is the process of expressing a composite number (a number greater than 1 that is not prime) as a product of its prime factors. Each composite number has a unique prime factorization, meaning there's only one way to express it as a product of primes (ignoring the order of the factors). This is known as the Fundamental Theorem of Arithmetic.
The Process of Prime Factorization
Several methods exist for performing prime factorization. The most common and intuitive method involves repeated division by prime numbers. Let's illustrate this with a simple example: finding the prime factorization of 12.
- Start with the smallest prime number, 2: 12 is divisible by 2 (12 / 2 = 6).
- Continue with the quotient: Now we work with 6. 6 is also divisible by 2 (6 / 2 = 3).
- The next quotient is a prime number: 3 is a prime number. We've reached the end of our factorization.
Therefore, the prime factorization of 12 is 2 x 2 x 3, or 2² x 3.
Finding the Prime Factorization of 420
Now, let's apply this method to find the prime factorization of 420:
- Divide by 2: 420 / 2 = 210
- Divide by 2 again: 210 / 2 = 105
- Divide by 3: 105 / 3 = 35
- Divide by 5: 35 / 5 = 7
- 7 is a prime number: We've reached a prime number.
Therefore, the prime factorization of 420 is 2 x 2 x 3 x 5 x 7, which can also be written as 2² x 3 x 5 x 7.
Applications of Prime Factorization
The seemingly simple act of finding the prime factorization of a number has surprisingly far-reaching applications:
- Greatest Common Divisor (GCD): Finding the GCD of two or more numbers is crucial in various mathematical and computational tasks. Prime factorization simplifies this process. By finding the prime factorization of each number, the GCD is simply the product of the common prime factors raised to the lowest power.
- Least Common Multiple (LCM): Similar to GCD, finding the LCM is simplified using prime factorization. The LCM is the product of all prime factors raised to the highest power present in the factorizations of the numbers.
- Simplifying Fractions: Prime factorization helps in simplifying fractions to their lowest terms. By factoring the numerator and denominator, common factors can be canceled out.
- Solving Diophantine Equations: These equations involve finding integer solutions. Prime factorization often plays a crucial role in solving certain types of Diophantine equations.
Advanced Techniques for Prime Factorization
For larger numbers, the method of repeated division becomes increasingly inefficient. More sophisticated algorithms are needed for efficient factorization. These include:
- Trial Division: A systematic method of testing divisibility by prime numbers up to the square root of the number.
- Pollard's Rho Algorithm: A probabilistic algorithm that is more efficient than trial division for larger numbers.
- General Number Field Sieve (GNFS): Currently, the most efficient algorithm known for factoring extremely large numbers, crucial for breaking certain cryptographic systems.
Conclusion: The Enduring Significance of Prime Factorization
The prime factorization of 420, while seemingly a simple problem, underscores the fundamental importance of prime numbers and factorization in mathematics and computer science. From simple calculations to complex cryptographic systems, the ability to decompose numbers into their prime components remains a cornerstone of many essential computational processes. Understanding this seemingly simple concept opens a world of deeper mathematical exploration and practical applications. The seemingly simple answer – 2² x 3 x 5 x 7 – represents a fundamental building block of number theory and countless applications beyond.
Latest Posts
Latest Posts
-
What Is 108 Inches In Feet
Apr 03, 2025
-
Aluminum Foil Hydrochloric Acid Balanced Equation
Apr 03, 2025
-
How Many Sides Does An Octogon Have
Apr 03, 2025
-
The Pectoral Girdle Consists Of The
Apr 03, 2025
-
Find The Unit Vector In The Direction Of V
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about What Is The Prime Factorization Of 420 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
