What Is The Prime Factorization Of 350
Juapaving
Mar 31, 2025 · 4 min read
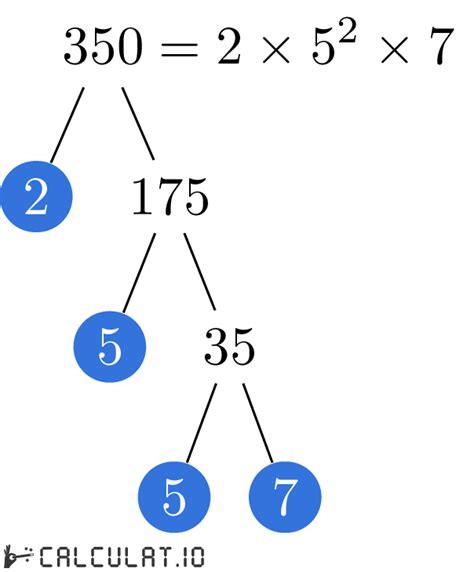
Table of Contents
What is the Prime Factorization of 350? A Deep Dive into Prime Numbers and Factorization
Finding the prime factorization of a number might seem like a simple mathematical exercise, but it’s a fundamental concept with far-reaching applications in number theory, cryptography, and computer science. Let's explore the prime factorization of 350, examining the process step-by-step and delving into the broader significance of prime numbers and factorization.
Understanding Prime Numbers and Prime Factorization
Before we tackle the prime factorization of 350, let's clarify some key terms:
-
Prime Number: A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. Examples include 2, 3, 5, 7, 11, and so on. The number 1 is not considered a prime number.
-
Composite Number: A composite number is a positive integer that has at least one divisor other than 1 and itself. All composite numbers can be expressed as a product of prime numbers.
-
Prime Factorization: The prime factorization of a composite number is the expression of that number as a product of its prime factors. This representation is unique for each composite number (excluding the order of the factors).
Finding the Prime Factorization of 350: A Step-by-Step Approach
Now, let's find the prime factorization of 350. We can use a method called the factor tree to systematically break down the number into its prime components.
-
Start with the given number: We begin with 350.
-
Find the smallest prime factor: The smallest prime number is 2. Since 350 is an even number, it's divisible by 2. Dividing 350 by 2, we get 175.
-
Continue factoring: Now we have 2 x 175. 175 is not divisible by 2. Let's try the next prime number, 3. The sum of the digits of 175 (1 + 7 + 5 = 13) is not divisible by 3, so 175 is not divisible by 3.
-
Trying the next prime number: The next prime number is 5. 175 is divisible by 5 (175 / 5 = 35). This gives us 2 x 5 x 35.
-
Factoring further: We now need to factor 35. It's divisible by 5 (35 / 5 = 7). This results in 2 x 5 x 5 x 7.
-
All factors are prime: We've reached a point where all factors (2, 5, 5, and 7) are prime numbers. Therefore, the prime factorization of 350 is complete.
The Prime Factorization of 350: 2 x 5² x 7
Therefore, the prime factorization of 350 is 2 x 5² x 7. This means 350 can be expressed as the product of one 2, two 5s, and one 7. This representation is unique to 350.
Applications of Prime Factorization
While seemingly simple, prime factorization has significant practical applications in various fields:
1. Cryptography:
Prime factorization forms the basis of many modern encryption algorithms. The difficulty of factoring very large numbers into their prime components is the foundation of the RSA algorithm, a widely used public-key cryptosystem that secures online transactions and communication. The security of these systems depends on the computational complexity of factoring large numbers – a task that becomes exponentially harder as the size of the number increases.
2. Number Theory:
Prime factorization is a cornerstone of number theory, a branch of mathematics that studies the properties of integers. It's crucial in understanding concepts like modular arithmetic, congruences, and the distribution of prime numbers. Many number-theoretic theorems and proofs rely heavily on prime factorization.
3. Computer Science:
Prime factorization algorithms are used in various computer science applications, including:
-
Hashing: Prime numbers are frequently used in hash table implementations to minimize collisions and improve efficiency.
-
Random Number Generation: Prime numbers play a role in designing efficient and high-quality pseudo-random number generators.
-
Data Compression: Certain data compression techniques utilize prime factorization to optimize data storage.
4. Mathematics Education:
Understanding prime factorization helps build a strong foundation in mathematics. It improves problem-solving skills, strengthens number sense, and lays the groundwork for more advanced mathematical concepts.
Alternative Methods for Prime Factorization
While the factor tree method is visually intuitive, other methods can be used to find the prime factorization of a number:
-
Division Method: This involves repeatedly dividing the number by the smallest prime number that divides it until you reach 1.
-
Algorithm-based methods: For very large numbers, sophisticated algorithms like the Pollard rho algorithm or the general number field sieve are employed to find prime factors efficiently. These algorithms are computationally intensive and require specialized software.
Conclusion: The Importance of Prime Factorization in a Digital World
The prime factorization of 350, seemingly a simple calculation, reveals a fundamental concept with profound implications in various fields. From securing online transactions to advancing our understanding of numbers, prime factorization plays a crucial role in both theoretical mathematics and practical applications. The ability to efficiently find the prime factors of a number is a problem with significant computational challenges, which underscores its importance in securing modern digital systems and pushing the boundaries of mathematical exploration. Understanding prime factorization is not just about solving a mathematical problem; it's about grasping a fundamental building block of the digital world we inhabit.
Latest Posts
Latest Posts
-
The Property Of Letting Light Pass Through Something
Apr 02, 2025
-
What Are The Greatest Common Factors Of 75
Apr 02, 2025
-
Do Parallelograms Have 4 Equal Sides
Apr 02, 2025
-
What Is Group Of Baboons Called
Apr 02, 2025
-
Exterior Angle Of A Regular Octagon
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is The Prime Factorization Of 350 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
