Exterior Angle Of A Regular Octagon
Juapaving
Apr 02, 2025 · 5 min read
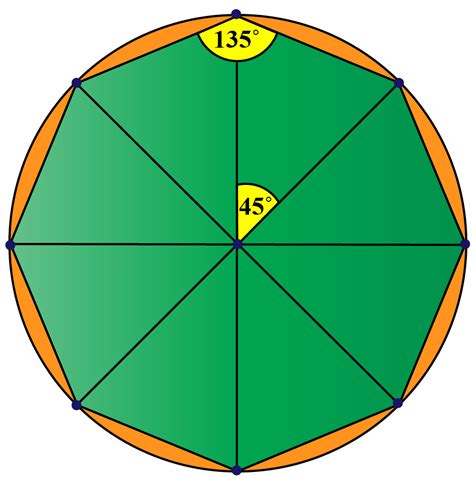
Table of Contents
Exterior Angle of a Regular Octagon: A Comprehensive Guide
The exterior angle of a regular octagon is a fundamental concept in geometry, with applications extending beyond theoretical mathematics into practical fields like architecture, engineering, and design. This comprehensive guide will delve into the properties of regular octagons, thoroughly explore the calculation of their exterior angles, and provide practical examples illustrating their real-world significance. We'll also touch upon related concepts and offer some problem-solving strategies.
Understanding Regular Octagons
Before diving into the exterior angle calculations, let's establish a firm understanding of what constitutes a regular octagon. A polygon is a closed two-dimensional shape with straight sides. An octagon, specifically, is a polygon with eight sides. The term "regular" adds a crucial element:
- Equal Sides: All eight sides of a regular octagon are of equal length.
- Equal Angles: All eight interior angles of a regular octagon are also equal in measure.
This uniformity simplifies calculations significantly, allowing us to derive predictable relationships between interior and exterior angles.
Calculating the Exterior Angle of a Regular Octagon
The exterior angle of any polygon is the angle formed by extending one of its sides. Imagine standing at a vertex of the octagon and walking along one side. The exterior angle is the angle you turn to walk along the next side. In a regular octagon, each exterior angle has the same measure.
There are several methods to calculate the exterior angle of a regular octagon:
Method 1: Using the Sum of Exterior Angles
A fundamental property of any polygon is that the sum of its exterior angles (one at each vertex) always equals 360 degrees. Since a regular octagon has eight equal exterior angles, we can calculate the measure of a single exterior angle by dividing the total sum by the number of sides:
Exterior Angle = 360° / Number of Sides
For a regular octagon:
Exterior Angle = 360° / 8 = 45°
Therefore, each exterior angle of a regular octagon measures 45 degrees.
Method 2: Using Interior Angles
Another approach involves utilizing the relationship between interior and exterior angles. Interior and exterior angles at the same vertex are supplementary; they add up to 180 degrees. First, we need to find the measure of each interior angle of a regular octagon.
The sum of the interior angles of any polygon can be calculated using the formula:
Sum of Interior Angles = (n - 2) * 180°
where 'n' is the number of sides. For an octagon (n = 8):
Sum of Interior Angles = (8 - 2) * 180° = 6 * 180° = 1080°
Since it's a regular octagon, each interior angle is equal:
Interior Angle = Sum of Interior Angles / Number of Sides
Interior Angle = 1080° / 8 = 135°
Finally, to find the exterior angle, subtract the interior angle from 180°:
Exterior Angle = 180° - Interior Angle = 180° - 135° = 45°
This confirms our earlier result: each exterior angle of a regular octagon measures 45 degrees.
Practical Applications of Exterior Angles
The concept of exterior angles, particularly in regular octagons, finds numerous applications in various fields:
Architecture and Design
- Tessellations: Regular octagons, when combined with other shapes (often squares), can create visually appealing and structurally sound tessellations (tilings) in flooring, wall designs, and other architectural elements. Understanding the exterior angles is crucial for ensuring proper fitting and avoiding gaps or overlaps.
- Building Structures: The angles are important in constructing frameworks and determining the precise cuts needed for beams and supports.
- Urban Planning: Octagonal shapes appear in city planning, particularly in designing roundabouts and traffic intersections for efficient traffic flow. Precise angle calculations are vital for optimizing space and minimizing congestion.
Engineering
- Gear Design: The precise angles are essential in designing gear systems, ensuring smooth meshing and efficient power transmission. Octagonal gears, though less common than circular ones, find specialized applications in machinery where specific angular movements are required.
- Robotics: In robotics, understanding the exterior angles helps in programming robotic arms or manipulators to perform specific movements and navigate complex paths.
- Mechanical Design: Octagonal shapes are sometimes used in mechanical components, and accurate angle measurements are necessary for proper assembly and functioning.
Other Applications
- Computer Graphics: The geometry of octagons, including their exterior angles, is crucial for creating realistic computer graphics and models, especially in games and simulations.
- Cartography: Understanding geometric properties like exterior angles aids in map-making and geographic information systems (GIS) for accurately representing landmasses and features.
- Art and Design: The visual symmetry and unique properties of octagons make them appealing to artists and designers, influencing various forms of art, from mosaics to illustrations.
Problem Solving and Further Exploration
Let's consider some example problems to solidify our understanding:
Problem 1: A regular octagonal tile needs to be fitted into a corner. What angle should be cut from one side of the tile to ensure a perfect fit against a 90-degree corner?
Solution: A regular octagon's exterior angle is 45°. To fit perfectly into a 90° corner, you need to cut an angle of 90° - 45° = 45° from one side of the tile.
Problem 2: An octagonal gazebo is being built with each side measuring 2 meters. Calculate the total perimeter.
Solution: The perimeter of any polygon is the sum of its side lengths. In a regular octagon, all sides are equal. Therefore, the perimeter is 8 sides * 2 meters/side = 16 meters.
Problem 3: A stop sign is shaped like a regular octagon. If the total sum of its interior angles is 1080°, what is the measure of each interior angle?
Solution: Since it's a regular octagon, all interior angles are equal. Dividing the sum of interior angles (1080°) by the number of sides (8) gives us 135° per interior angle.
Beyond Regular Octagons: Irregular Octagons
It's important to note that the calculations we've performed apply specifically to regular octagons. Irregular octagons, where sides and angles are not equal, require different approaches. Finding exterior angles in an irregular octagon involves calculating each exterior angle individually, often using trigonometry or vector methods depending on the available information about the polygon's dimensions.
Conclusion
The exterior angle of a regular octagon, consistently measuring 45 degrees, is a fundamental concept with wide-ranging practical applications. Understanding this angle, along with the relationships between interior and exterior angles, provides a foundation for solving problems in diverse fields, from architecture and engineering to computer graphics and art. By mastering these concepts, you'll develop a deeper appreciation for the geometric principles that shape the world around us. The seemingly simple calculation holds a surprising amount of practical power, highlighting the beauty and utility of geometric principles.
Latest Posts
Latest Posts
-
How Tall Is 48 Inches In Ft
Apr 03, 2025
-
What Is A Strait In Geography
Apr 03, 2025
-
Which Of The Following Is A Multiple Of 2
Apr 03, 2025
-
Examples Of Elements In Everyday Life
Apr 03, 2025
-
Least Common Multiple Of 7 And 11
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Exterior Angle Of A Regular Octagon . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
