Do Parallelograms Have 4 Equal Sides
Juapaving
Apr 02, 2025 · 5 min read
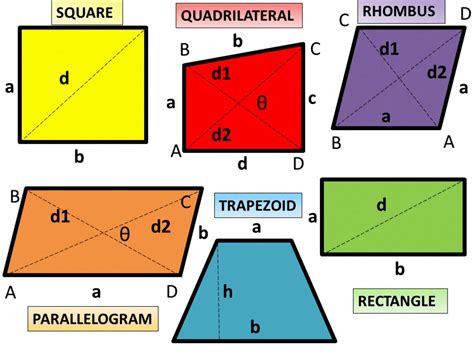
Table of Contents
Do Parallelograms Have 4 Equal Sides? Understanding Quadrilateral Properties
The question of whether parallelograms possess four equal sides is a fundamental concept in geometry. The short answer is: no, not all parallelograms have four equal sides. While some parallelograms do have four equal sides, this is a specific case, not a defining characteristic of all parallelograms. This article will delve deep into the properties of parallelograms, contrasting them with other quadrilaterals, and clarifying the conditions under which a parallelogram might also possess four equal sides.
Defining Parallelograms: Key Properties
A parallelogram is a quadrilateral, meaning a two-dimensional closed shape with four sides. However, what distinguishes a parallelogram from other quadrilaterals are its specific properties:
- Opposite sides are parallel: This is the defining characteristic. The opposite sides of a parallelogram are parallel to each other. This parallelism is crucial for understanding other properties.
- Opposite sides are equal in length: While not the defining property, opposite sides of a parallelogram are always congruent (equal in length). This stems directly from the parallel property.
- Opposite angles are equal: Similar to side lengths, the angles opposite each other within a parallelogram are always equal in measure.
- Consecutive angles are supplementary: Consecutive angles (angles next to each other) add up to 180 degrees. This is a direct consequence of parallel lines and transversal lines.
- Diagonals bisect each other: The diagonals of a parallelogram intersect at their midpoints. This means each diagonal cuts the other in half.
Differentiating Parallelograms from Other Quadrilaterals
To fully grasp the concept, it's essential to compare parallelograms with other quadrilaterals:
1. Rectangles:
Rectangles are a special type of parallelogram. They possess all the properties of a parallelogram, plus the additional characteristic that all four angles are right angles (90 degrees). Note that a rectangle doesn't necessarily have four equal sides; only a square does.
2. Rhombuses:
A rhombus is another special case of a parallelogram. It shares all the parallelogram properties but adds the crucial difference that all four sides are equal in length. This makes it distinct from other parallelograms. A rhombus's angles, however, are not necessarily right angles.
3. Squares:
A square is a highly specific quadrilateral. It is both a rectangle and a rhombus. Therefore, it possesses all the properties of a parallelogram, rectangle, and rhombus. Crucially, a square has four equal sides and four right angles.
4. Trapezoids (Trapeziums):
Unlike parallelograms, trapezoids only have one pair of parallel sides. They do not necessarily have equal opposite sides or equal angles.
5. Kites:
Kites have two pairs of adjacent sides that are equal in length. Unlike parallelograms, their opposite sides are not parallel, nor are their opposite angles equal.
When a Parallelogram Has Four Equal Sides: The Rhombus
As previously mentioned, the only instance where a parallelogram automatically has four equal sides is when it's a rhombus. The term "rhombus" itself implies this property. Any quadrilateral that fulfills the conditions for a parallelogram and has all four sides of equal length is, by definition, a rhombus.
This makes the rhombus a unique and important case within the broader family of parallelograms. Understanding its characteristics is essential for differentiating it from other types of parallelograms.
Visualizing the Differences: Diagrams and Examples
Visual representations are crucial for understanding these geometric concepts. Imagine different shapes:
- A typical parallelogram: This might have two longer parallel sides and two shorter parallel sides. The opposite sides are equal, but not all four sides are the same length.
- A rectangle: This has four right angles, with opposite sides being equal. It could be a long, thin rectangle, illustrating that it doesn’t need to have four equal sides.
- A rhombus: This would have four equal sides, but the angles are not necessarily right angles. It could be quite "squashed" or stretched, emphasizing the equal-side property.
- A square: This has both four equal sides and four right angles, combining the features of a rectangle and a rhombus.
By visualizing these different types, the distinction between parallelograms with and without four equal sides becomes clearer.
Applications and Real-World Examples
The properties of parallelograms and their specific cases (rectangles, rhombuses, squares) have many applications in various fields:
- Engineering: Parallelogram structures are used in bridges, buildings, and mechanical systems due to their stability and strength.
- Architecture: The shapes are evident in building designs and frameworks.
- Art and Design: Parallelograms appear in artistic compositions and designs, often for visual balance and symmetry.
- Computer Graphics: The properties are fundamental to creating and manipulating two-dimensional shapes and images.
Understanding the subtle differences between these quadrilateral types is critical for accurate calculations and designs in these real-world scenarios.
Advanced Concepts and Further Exploration
For a deeper understanding, consider exploring these advanced concepts:
- Vectors and Parallelograms: The geometric properties of parallelograms can be elegantly described using vectors.
- Area Calculations: The formulas for calculating the area of parallelograms, rectangles, rhombuses, and squares.
- Coordinate Geometry: Representing and analyzing parallelograms using coordinate systems.
Conclusion: Parallelograms and the Four Equal Sides Myth
In conclusion, while some parallelograms do have four equal sides, this is not a defining characteristic of all parallelograms. The defining properties of a parallelogram are the parallelism of its opposite sides and the equality of its opposite sides. A parallelogram with four equal sides is specifically classified as a rhombus. Understanding the nuances between parallelograms, rectangles, rhombuses, and squares is crucial for mastering geometric concepts and their applications. Remembering this distinction will avoid common misconceptions surrounding these fundamental shapes.
Latest Posts
Latest Posts
-
A Homogeneous Mixture Is Also Called A
Apr 03, 2025
-
A Substance Formed During A Chemical Reaction
Apr 03, 2025
-
Give The Major Product Of The Following Reaction
Apr 03, 2025
-
An Npn Transistor Is Made Up Of
Apr 03, 2025
-
How Tall Is 48 Inches In Ft
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Do Parallelograms Have 4 Equal Sides . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
