What Is The Prime Factorization For 63
Juapaving
Mar 31, 2025 · 5 min read
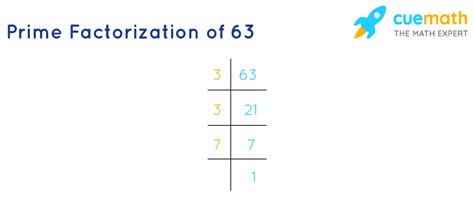
Table of Contents
What is the Prime Factorization for 63? A Deep Dive into Prime Numbers and Factorization
Finding the prime factorization of a number might seem like a simple task, especially for smaller numbers like 63. However, understanding the underlying principles of prime numbers and factorization is crucial for grasping more complex mathematical concepts. This article will delve into the prime factorization of 63, explaining the process step-by-step and exploring the broader significance of prime numbers in mathematics and computer science.
Understanding Prime Numbers
Before we tackle the prime factorization of 63, let's define what a prime number is. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. This means it cannot be expressed as a product of two smaller whole numbers. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on. Note that 1 is not considered a prime number.
Conversely, a composite number is a whole number greater than 1 that is not prime. This means it can be factored into smaller whole numbers. For example, 6 is a composite number because it can be factored into 2 x 3.
The fundamental theorem of arithmetic states that every integer greater than 1 can be represented uniquely as a product of prime numbers, ignoring the order of the factors. This theorem is the cornerstone of prime factorization and has significant implications across various mathematical fields.
Finding the Prime Factorization of 63
Now, let's find the prime factorization of 63. We can do this using a method called the factor tree.
-
Start with the number: Begin with the number 63.
-
Find a pair of factors: Find two numbers that multiply to give 63. A simple pair is 7 and 9. We can write this as: 63 = 7 x 9
-
Continue factoring: Now, check if the factors themselves are prime. 7 is a prime number (its only factors are 1 and 7). However, 9 is a composite number (3 x 3). So we continue factoring 9: 9 = 3 x 3
-
Identify the prime factors: We've now broken down 63 into its prime factors: 3, 3, and 7.
-
Write the prime factorization: We can express the prime factorization of 63 as 3² x 7. This means 63 is the product of two 3s and one 7.
Therefore, the prime factorization of 63 is 3² x 7.
Visualizing with a Factor Tree
A factor tree visually represents the process of finding the prime factorization. Here's what the factor tree for 63 would look like:
63
/ \
7 9
/ \
3 3
The bottom branches of the tree represent the prime factors.
Alternative Methods for Prime Factorization
While the factor tree is a visually intuitive method, other methods exist for finding prime factorizations, particularly for larger numbers.
-
Division by primes: Start dividing the number by the smallest prime number (2), and continue dividing by successively larger prime numbers (3, 5, 7, etc.) until you reach 1. The prime numbers you used are the prime factors.
-
Using algorithms: For very large numbers, sophisticated algorithms are employed to find prime factorizations. These algorithms are crucial in cryptography and cybersecurity.
The Significance of Prime Factorization
The seemingly simple process of prime factorization has far-reaching consequences across numerous fields:
1. Cryptography: RSA Algorithm
The RSA algorithm, a widely used public-key cryptosystem, relies heavily on the difficulty of factoring large composite numbers into their prime factors. The security of the RSA algorithm hinges on the computational infeasibility of factoring extremely large numbers with hundreds or even thousands of digits. This makes it a cornerstone of secure online communication and e-commerce.
2. Number Theory: Fundamental Theorem of Arithmetic
As mentioned earlier, the fundamental theorem of arithmetic guarantees that every integer greater than 1 has a unique prime factorization. This seemingly simple statement is fundamental to many advanced mathematical concepts and theorems. It provides a structure for understanding and manipulating integers.
3. Computer Science: Algorithms and Data Structures
Prime factorization algorithms are used in various computer science applications, including:
- Hashing: Prime numbers are often used in hash table implementations to minimize collisions.
- Random Number Generation: Prime numbers play a role in creating pseudo-random number generators.
- Error Detection and Correction: Certain error-correcting codes utilize prime numbers.
4. Modular Arithmetic: Congruences and Residues
Prime numbers and prime factorization are essential in modular arithmetic. Modular arithmetic, which involves working with remainders after division, forms the basis of many cryptographic algorithms and other mathematical applications.
Prime Factorization Beyond 63: Examples and Practice
Let's explore the prime factorization of a few other numbers to solidify our understanding:
- 12: 12 = 2² x 3
- 24: 24 = 2³ x 3
- 36: 36 = 2² x 3²
- 100: 100 = 2² x 5²
- 1000: 1000 = 2³ x 5³
Practice finding the prime factorization of different numbers using the factor tree or division by primes. This will build your intuition and understanding of prime numbers and factorization.
Conclusion: The Enduring Importance of Prime Numbers
The prime factorization of 63, while seemingly straightforward, provides a valuable entry point into a vast and complex world of number theory and its applications. Understanding prime numbers and their properties is crucial for comprehending many fundamental mathematical concepts and for appreciating their importance in computer science, particularly in the realm of cryptography and security. The unique factorization property, the backbone of many sophisticated algorithms, ensures the secure functioning of online systems that we rely on daily. From the seemingly simple task of factoring 63 to the complex algorithms protecting online transactions, the world of prime numbers and factorization is both fascinating and profoundly impactful.
Latest Posts
Latest Posts
-
What Are Aerial Parts Of A Plant
Apr 01, 2025
-
What Is The Difference Between Absorption And Emission Spectrum
Apr 01, 2025
-
What Is The Waste Product Of Photosynthesis
Apr 01, 2025
-
Sound Travels Fastest In Which Medium
Apr 01, 2025
-
What Are The Two Parts Of An Atom
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Is The Prime Factorization For 63 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
