What Is The Percent Of 3/20
Juapaving
Mar 26, 2025 · 5 min read
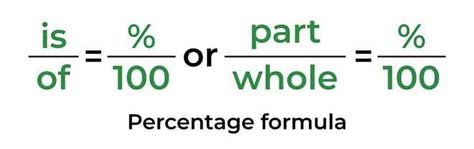
Table of Contents
What is the Percent of 3/20? A Comprehensive Guide to Percentage Conversions
Understanding percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and tips to understanding financial reports and statistical data. This comprehensive guide will delve into the process of converting fractions to percentages, focusing specifically on the fraction 3/20, and exploring various methods to achieve this conversion. We'll also discuss the significance of percentages in different contexts and provide practical examples to solidify your understanding.
Understanding Fractions and Percentages
Before we dive into calculating the percentage equivalent of 3/20, let's clarify the basics.
Fractions: A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts we're considering, while the denominator indicates the total number of equal parts that make up the whole. For example, in the fraction 3/20, 3 is the numerator and 20 is the denominator.
Percentages: A percentage is a way of expressing a number as a fraction of 100. The symbol "%" is used to represent percentage. It indicates how many parts per hundred are being considered. For example, 50% means 50 parts out of 100, or 50/100, which simplifies to 1/2.
Method 1: Converting the Fraction to a Decimal
The most common method for converting a fraction to a percentage involves first converting the fraction to a decimal. This is done by dividing the numerator by the denominator.
-
Divide the numerator by the denominator: In our case, we divide 3 by 20: 3 ÷ 20 = 0.15
-
Multiply the decimal by 100: To express the decimal as a percentage, we multiply it by 100: 0.15 x 100 = 15
-
Add the percentage symbol: The final result is 15%.
Therefore, 3/20 is equal to 15%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
Another approach involves finding an equivalent fraction where the denominator is 100. This method directly gives us the percentage since a percentage is a fraction out of 100.
-
Determine the multiplication factor: To change the denominator of 3/20 to 100, we need to determine what number we must multiply 20 by to get 100. This is 5 (20 x 5 = 100).
-
Multiply both the numerator and denominator: To maintain the value of the fraction, we must multiply both the numerator and the denominator by the same number (5 in this case): (3 x 5) / (20 x 5) = 15/100
-
Express as a percentage: Since the denominator is now 100, the numerator directly represents the percentage: 15/100 = 15%.
Method 3: Using Proportions
Proportions offer a powerful method for solving percentage problems. A proportion sets up an equality between two ratios.
-
Set up the proportion: We can set up a proportion as follows:
3/20 = x/100
Where 'x' represents the percentage we're trying to find.
-
Cross-multiply: To solve for 'x', we cross-multiply:
20x = 300
-
Solve for x: Divide both sides by 20:
x = 300 ÷ 20 = 15
Therefore, x = 15, meaning 3/20 is equal to 15%.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial in numerous real-world scenarios. Here are a few examples:
-
Discounts: If a store offers a 15% discount on an item, you can easily calculate the discount amount by multiplying the item's price by 0.15. Understanding that 3/20 is equal to 15% helps you quickly estimate the discount without needing a calculator in some situations.
-
Taxes: Sales tax is typically expressed as a percentage. Calculating the tax amount involves multiplying the price of the item by the tax rate.
-
Tips: When dining out, calculating a tip (e.g., 15% or 20%) based on the total bill requires understanding percentage calculations.
-
Financial Statements: Financial statements, such as income statements and balance sheets, are filled with percentages that represent ratios and proportions of various financial figures. These percentages help in understanding the financial health of a company or individual.
-
Statistics: Percentages are essential in statistics for representing data, making comparisons, and drawing conclusions from data sets.
Advanced Concepts and Related Calculations
While converting 3/20 to a percentage is relatively straightforward, let's explore some related calculations that build upon this foundation:
-
Calculating the Percentage Increase or Decrease: If a value changes from one point to another, you can calculate the percentage increase or decrease using the formula: [(New Value - Old Value) / Old Value] x 100.
-
Finding a Percentage of a Number: To find a percentage of a number, simply multiply the number by the percentage (expressed as a decimal). For instance, finding 15% of 200 would be 200 x 0.15 = 30.
-
Working Backwards from a Percentage: If you know a percentage and the resulting value, you can work backward to find the original value. For example, if 15% of a number is 30, the original number can be found by dividing 30 by 0.15, resulting in 200.
-
Compound Percentage Changes: In some scenarios, percentages are applied multiple times. This is known as compound percentage change. For example, calculating interest on an investment where the interest is compounded annually involves successive applications of percentages.
-
Percentage Points: It is important to note the difference between percentage change and percentage points. A change from 20% to 25% represents a 5 percentage point increase, but a 25% increase relative to the initial value. Understanding this distinction is crucial for accurate interpretation of data and financial reports.
Conclusion
Converting fractions to percentages is a fundamental skill with significant practical implications across various fields. We've explored multiple methods for converting 3/20 to its percentage equivalent, which is 15%. By mastering these techniques and understanding the concepts behind percentage calculations, you can confidently handle a wide range of percentage-related problems, improving your analytical skills and problem-solving abilities in both academic and professional contexts. Remember that consistent practice and application of these methods will lead to a stronger grasp of percentage conversions and their application in real-world situations.
Latest Posts
Latest Posts
-
What Is The Gcf Of 18 And 12
Mar 29, 2025
-
What Is Commonly Called The King Of Spices
Mar 29, 2025
-
How To Find Inverse Of A Relation
Mar 29, 2025
-
What Is The Lowest Common Multiple Of 2 And 3
Mar 29, 2025
-
What Is The Electron Configuration Of Rubidium
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about What Is The Percent Of 3/20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
