What Is The Lowest Common Multiple Of 7 And 9
Juapaving
Mar 29, 2025 · 5 min read
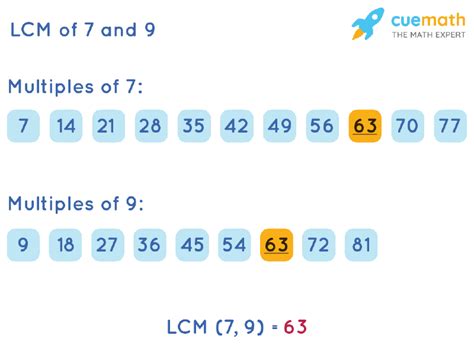
Table of Contents
What is the Lowest Common Multiple (LCM) of 7 and 9? A Deep Dive into Finding LCMs
Finding the lowest common multiple (LCM) might seem like a simple arithmetic task, especially when dealing with small numbers like 7 and 9. However, understanding the underlying concepts and different methods for calculating LCMs is crucial for a strong foundation in mathematics and its applications. This comprehensive guide will explore what the LCM of 7 and 9 is, delve into various methods for calculating LCMs, and examine the broader significance of LCMs in various fields.
Understanding Lowest Common Multiples (LCMs)
Before jumping into the calculation for the LCM of 7 and 9, let's define what an LCM actually is. The lowest common multiple, or LCM, of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly without leaving a remainder.
For example, consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12, 14... and multiples of 3 are 3, 6, 9, 12, 15... The smallest number that appears in both lists is 6. Therefore, the LCM of 2 and 3 is 6.
Calculating the LCM of 7 and 9: Methods and Approaches
There are several methods to determine the LCM of 7 and 9. We'll explore the most common and effective techniques:
1. Listing Multiples Method
This is the most straightforward approach, especially for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70...
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81...
Notice that the smallest number that appears in both lists is 63. Therefore, the LCM of 7 and 9 is 63.
This method is simple to understand but can become cumbersome and time-consuming for larger numbers.
2. Prime Factorization Method
This method involves breaking down each number into its prime factors. The prime factorization of a number is its representation as a product of prime numbers.
- Prime factorization of 7: 7 (7 is a prime number itself)
- Prime factorization of 9: 3 x 3 = 3²
To find the LCM using prime factorization, we take the highest power of each prime factor present in the factorizations:
- The prime factors are 3 and 7.
- The highest power of 3 is 3² = 9.
- The highest power of 7 is 7¹ = 7.
Therefore, the LCM is 3² x 7 = 9 x 7 = 63.
This method is more efficient than listing multiples, especially when dealing with larger numbers. It provides a structured approach that's less prone to error.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (greatest common divisor) of two numbers are related. The product of the LCM and GCD of two numbers is equal to the product of the two numbers. That is:
LCM(a, b) * GCD(a, b) = a * b
First, we find the GCD of 7 and 9 using the Euclidean algorithm or prime factorization. Since 7 and 9 have no common factors other than 1, their GCD is 1.
Then, using the formula:
LCM(7, 9) = (7 * 9) / GCD(7, 9) = 63 / 1 = 63
This method is particularly useful when the GCD is easily determined.
Significance and Applications of LCMs
The concept of LCMs extends far beyond simple arithmetic exercises. It finds practical applications in various fields:
1. Scheduling and Time Management:
Imagine two buses leaving a station at different intervals. One bus leaves every 7 minutes, and another leaves every 9 minutes. To find out when both buses will leave at the same time again, you need to find the LCM of 7 and 9. The LCM (63 minutes) represents the time it takes for both buses to leave simultaneously. This principle applies to various scheduling problems, from production lines to traffic light synchronization.
2. Fraction Operations:
LCMs are crucial for adding and subtracting fractions with different denominators. To add fractions, you must find a common denominator, which is typically the LCM of the denominators. This ensures that you're working with equivalent fractions that can be easily added or subtracted.
3. Music Theory:
In music, LCMs are used to determine the least common period of overlapping rhythmic patterns. Understanding the LCM of note durations helps in composing complex musical pieces with harmonizing rhythms.
4. Gear Ratios and Mechanical Systems:
In engineering and mechanics, LCMs are employed in calculating gear ratios and the synchronization of rotating components in machinery. Determining the LCM helps in optimizing the efficiency and smooth operation of mechanical systems.
5. Computer Science and Algorithms:
LCMs appear in various algorithms, particularly those dealing with cyclic processes, synchronization, and resource allocation. The ability to efficiently calculate LCMs is valuable in optimizing the performance of computer programs.
Beyond the Basics: Expanding the Concept of LCMs
While we've focused on the LCM of two numbers, the concept extends to finding the LCM of three or more numbers. The process involves similar methods, either using prime factorization or iterative approaches. For instance, to find the LCM of 7, 9, and 10:
-
Prime Factorization:
- 7 = 7
- 9 = 3²
- 10 = 2 x 5
-
LCM: The LCM will be 2 x 3² x 5 x 7 = 630
The ability to find the LCM efficiently is a fundamental skill in mathematics with wide-ranging practical applications.
Conclusion: Mastering LCMs for Mathematical Proficiency
Understanding the concept of the lowest common multiple and mastering different calculation methods is crucial for success in mathematics and its related fields. While the LCM of 7 and 9 might seem like a simple problem, the underlying principles and techniques extend to complex scenarios in various disciplines. By mastering these concepts, you’ll not only improve your mathematical proficiency but also equip yourself with valuable tools for problem-solving in diverse contexts. The methods discussed in this article – listing multiples, prime factorization, and using the GCD – offer a versatile toolkit for tackling LCM problems, regardless of the numbers involved. Remember, practice makes perfect! The more you work with LCMs, the more confident and proficient you will become.
Latest Posts
Latest Posts
-
Forward Primer And Reverse Primer In Pcr
Mar 31, 2025
-
Words That Begin With A H
Mar 31, 2025
-
Which Of The Following Is Not An Antibiotic
Mar 31, 2025
-
What Is Difference Between Football And Soccer
Mar 31, 2025
-
Explain The Differences Between Expressions And Equations
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lowest Common Multiple Of 7 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
