Explain The Differences Between Expressions And Equations.
Juapaving
Mar 31, 2025 · 5 min read
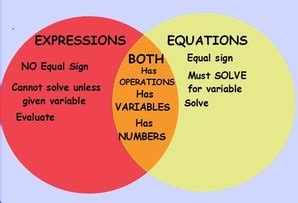
Table of Contents
Expressions vs. Equations: Unveiling the Core Differences
Mathematics, the language of logic and patterns, relies heavily on precise terminology. Two fundamental building blocks of mathematical communication are expressions and equations. While they might seem interchangeable at first glance, understanding their distinct characteristics is crucial for grasping more complex mathematical concepts. This article delves into the core differences between expressions and equations, exploring their structures, applications, and the implications of misinterpreting one for the other.
What is a Mathematical Expression?
A mathematical expression is a combination of numbers, variables, and mathematical operations (such as addition, subtraction, multiplication, division, exponents, and roots) that represents a single numerical value or a quantity. It doesn't state a relationship or make a claim; it simply represents a value. Think of it as a phrase in the language of mathematics.
Key Characteristics of Expressions:
- No equal sign (=): This is the most crucial distinction. Expressions lack an equal sign, indicating they are not making a statement of equality.
- Can be simplified or evaluated: Expressions can be simplified by combining like terms or evaluated by substituting values for the variables to obtain a numerical result.
- Represents a single value (potentially complex): Even expressions containing multiple operations ultimately represent a single, possibly complex, numerical value.
Examples of Expressions:
3x + 5(An algebraic expression with a variable)2 + 7 - 4(An arithmetic expression)√(16 + 9)(An expression involving a square root)(4 * 5) / 2(An expression with order of operations)x² - 4x + 4(A polynomial expression)
What is a Mathematical Equation?
A mathematical equation is a statement that asserts the equality of two expressions. It uses an equal sign (=) to declare that the expression on the left-hand side (LHS) is equivalent to the expression on the right-hand side (RHS). Think of it as a complete sentence in mathematical language, making a declarative statement.
Key Characteristics of Equations:
- Contains an equal sign (=): The presence of the equal sign is what fundamentally distinguishes an equation from an expression.
- Expresses a relationship: Equations show a relationship between two expressions, stating that they are equal.
- Can be solved: Equations can be solved to find the value(s) of the variable(s) that make the equation true. This process involves manipulating the equation using algebraic rules to isolate the variable.
- Can be conditional: The equality in an equation might only hold true for specific values of the variables involved.
Examples of Equations:
2x + 3 = 7(A linear equation)x² - 4 = 0(A quadratic equation)y = mx + b(The slope-intercept form of a linear equation)A = πr²(The equation for the area of a circle)E = mc²(Einstein's famous equation relating energy and mass)
Understanding the Nuances: Expressions within Equations
It's crucial to understand that expressions frequently appear within equations. The two sides of an equation are themselves expressions. The equation 2x + 5 = 11 contains two expressions: 2x + 5 on the left and 11 on the right. We solve the equation by manipulating the expressions to isolate the variable x.
This nested structure highlights the hierarchical relationship: equations are composed of expressions, but expressions themselves don't constitute equations unless connected by an equal sign.
The Significance of the Equal Sign
The equal sign is the linchpin that differentiates expressions from equations. It's not merely a symbol of equivalence; it's a declaration of a relationship. This seemingly simple symbol profoundly impacts how we interpret and manipulate mathematical statements. An incorrect use or interpretation of the equal sign can lead to significant errors in calculations and problem-solving.
Applications in Different Mathematical Fields
The distinction between expressions and equations is vital across diverse branches of mathematics:
Algebra:
In algebra, expressions are manipulated to simplify calculations and solve equations. The ability to identify expressions and understand their properties is fundamental to mastering algebraic techniques like factoring, expanding, and solving equations.
Calculus:
Calculus heavily relies on expressions, particularly functions. Derivatives and integrals are operations performed on expressions to analyze rates of change and accumulation, respectively. Equations arise when setting expressions equal to zero to find critical points or solving differential equations.
Geometry:
Geometric formulas are often expressed as equations. For example, the formula for the area of a triangle (A = (1/2)bh) is an equation relating the area (A) to the base (b) and height (h). However, expressions arise in the process of calculating areas using the formula.
Statistics:
Statistical calculations involve numerous expressions. Formulas for calculating mean, variance, and standard deviation are all composed of expressions. Equations arise when testing hypotheses or establishing relationships between variables.
Common Mistakes and Misunderstandings
A frequent error is confusing expressions with equations, especially when dealing with complex algebraic manipulations. For instance, mistakenly interpreting 3x + 2 as an equation instead of an expression leads to incorrect attempts at solving for x without additional context or a defining equality.
Another potential source of confusion is the use of multiple equal signs in a single line. While this is often acceptable for demonstrating a sequence of equivalent expressions, it's crucial to maintain awareness that each equal sign represents a separate statement of equality.
Practical Implications and Problem-Solving
The ability to distinguish between expressions and equations is paramount for successful problem-solving in mathematics. Proper identification allows for applying the appropriate mathematical techniques. Attempting to "solve" an expression is a fundamental misconception, as an expression does not possess a solution in the same way an equation does. Instead, expressions are simplified or evaluated.
Conclusion: Precision in Mathematical Language
Mathematical language demands precision. The difference between an expression and an equation is not a mere technicality; it forms the bedrock of understanding mathematical structures and operations. Mastering this distinction empowers students to navigate the complexities of algebra, calculus, and beyond with confidence and accuracy, laying a strong foundation for more advanced mathematical concepts. Consistent practice in recognizing and manipulating expressions and equations strengthens problem-solving abilities and cultivates a deeper understanding of the language of mathematics itself. Remembering the absence or presence of the equal sign is the key to successfully distinguishing between these two fundamental mathematical constructs.
Latest Posts
Latest Posts
-
What Is The Difference Between Lonely And Alone
Apr 02, 2025
-
What Is The Prime Factors Of 150
Apr 02, 2025
-
Hydrolysis Of Adp Produces Which Of The Following Products
Apr 02, 2025
-
Write Equations For Lines Of Best Fit Calculator
Apr 02, 2025
-
What Is Conjugate Acid Of Nh3
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Explain The Differences Between Expressions And Equations. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
