What Is The Lowest Common Multiple Of 5 And 7
Juapaving
Mar 30, 2025 · 5 min read
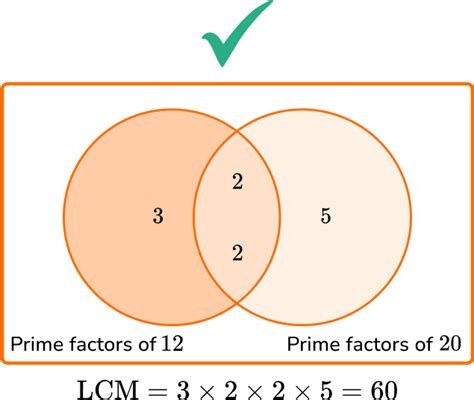
Table of Contents
What is the Lowest Common Multiple (LCM) of 5 and 7? A Deep Dive into Number Theory
Finding the lowest common multiple (LCM) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts reveals a fascinating glimpse into number theory. This article will explore the LCM of 5 and 7 in detail, examining various methods for calculating it and delving into the broader mathematical significance of this concept. We'll move beyond simply stating the answer and explore why this seemingly simple calculation is fundamental to more advanced mathematical operations.
Understanding the Fundamentals: Factors, Multiples, and the LCM
Before we tackle the LCM of 5 and 7, let's solidify our understanding of the core concepts.
Factors: The Building Blocks of Numbers
Factors are numbers that divide evenly into a larger number without leaving a remainder. For instance, the factors of 12 are 1, 2, 3, 4, 6, and 12. Understanding factors is crucial because they form the foundation for finding the LCM.
Multiples: Extending the Number Line
Multiples are the results of multiplying a number by integers (whole numbers). For example, the multiples of 5 are 5, 10, 15, 20, 25, and so on. Similarly, the multiples of 7 are 7, 14, 21, 28, 35, and so on.
The Lowest Common Multiple (LCM): Finding the Smallest Shared Multiple
The lowest common multiple (LCM) is the smallest positive integer that is a multiple of two or more numbers. It's the smallest number that all the given numbers divide into evenly. Understanding the LCM is vital in various applications, from simplifying fractions to solving problems in areas like scheduling and measurement.
Calculating the LCM of 5 and 7: Three Proven Methods
Now, let's explore three different approaches to find the LCM of 5 and 7.
Method 1: Listing Multiples
The simplest method involves listing the multiples of each number until we find the smallest common multiple.
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40...
- Multiples of 7: 7, 14, 21, 28, 35, 42...
As you can see, the smallest number that appears in both lists is 35. Therefore, the LCM of 5 and 7 is 35.
This method works well for smaller numbers, but it becomes increasingly cumbersome as the numbers get larger.
Method 2: Prime Factorization
This method utilizes the prime factorization of each number. Prime factorization is the process of expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
- Prime factorization of 5: 5 (5 is itself a prime number)
- Prime factorization of 7: 7 (7 is also a prime number)
Since 5 and 7 are both prime numbers and have no common factors other than 1, their LCM is simply their product: 5 x 7 = 35.
This method is more efficient than listing multiples, especially for larger numbers. It provides a deeper understanding of the numbers' structure and reveals the relationship between factors and multiples.
Method 3: Using the Formula (LCM(a,b) = |a*b| / GCD(a,b))
This method leverages the greatest common divisor (GCD) of the two numbers. The GCD is the largest number that divides both numbers without leaving a remainder.
- Finding the GCD of 5 and 7: Since 5 and 7 are prime numbers and share no common factors other than 1, their GCD is 1.
Now, we use the formula: LCM(a,b) = |a*b| / GCD(a,b)
LCM(5,7) = (5 * 7) / 1 = 35
This formula offers a concise and powerful way to calculate the LCM, especially when dealing with larger numbers where finding the GCD might be more challenging than listing multiples or using prime factorization alone. Understanding the GCD is essential for mastering this approach.
The Significance of the LCM Beyond Simple Calculation
The seemingly simple calculation of the LCM of 5 and 7 has far-reaching implications in various mathematical and real-world applications.
Applications in Fraction Arithmetic
The LCM plays a crucial role in adding and subtracting fractions. To add or subtract fractions, we need a common denominator, which is the LCM of the denominators. For example, to add 1/5 and 1/7, we find the LCM of 5 and 7 (which is 35) and then rewrite the fractions with this common denominator before adding them.
Scheduling and Cyclical Events
The LCM is incredibly useful in solving scheduling problems. Imagine two buses departing from the same station at different intervals. One bus departs every 5 minutes, and the other departs every 7 minutes. The LCM (35 minutes) represents the time it will take for both buses to depart simultaneously again.
Measurement and Unit Conversion
In measurement and unit conversion, the LCM can help find the smallest common unit for measurements with different denominators. This is particularly valuable in scenarios involving fractions of units.
Advanced Mathematical Concepts
The LCM forms the basis for more advanced mathematical concepts, including modular arithmetic and abstract algebra. These areas of mathematics have widespread applications in cryptography, computer science, and other fields.
Expanding the Concept: LCM of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For prime factorization, we simply find the prime factorization of each number and take the highest power of each prime factor present in any of the factorizations. For the formula method, we can extend it iteratively, finding the LCM of the first two numbers, then the LCM of that result and the third number, and so on. Listing multiples becomes significantly less efficient with more numbers.
Conclusion: The Unsung Hero of Number Theory
The LCM, although seemingly simple, is a fundamental concept with far-reaching applications. While finding the LCM of 5 and 7 might appear trivial, understanding the underlying principles and various methods for calculating it provides valuable insights into number theory and its practical applications. From simplifying fractions to solving complex scheduling problems, the LCM proves to be an unsung hero in the world of mathematics. Mastering this concept lays a solid foundation for more advanced mathematical explorations. This deeper understanding moves beyond a simple answer and reveals the elegance and power inherent in even the most basic mathematical concepts.
Latest Posts
Latest Posts
-
Blood Is A Compound Or Mixture
Apr 01, 2025
-
Compare And Contrast Hinduism And Buddhism
Apr 01, 2025
-
Why Is The Trachea Reinforced With Cartilaginous Rings
Apr 01, 2025
-
Least Common Multiple 3 And 8
Apr 01, 2025
-
Is Tearing Paper A Physical Change
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lowest Common Multiple Of 5 And 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
