Least Common Multiple 3 And 8
Juapaving
Apr 01, 2025 · 5 min read
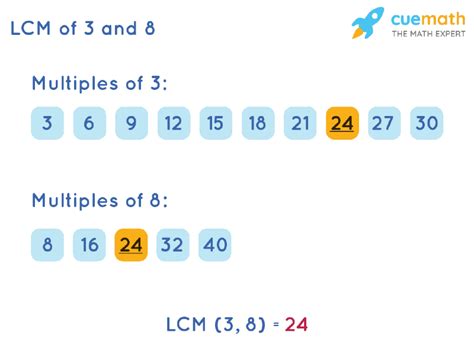
Table of Contents
Unveiling the Mysteries of the Least Common Multiple of 3 and 8: A Deep Dive
The concept of the Least Common Multiple (LCM) is a fundamental element in mathematics, particularly within number theory and algebra. Understanding LCMs is crucial for simplifying fractions, solving problems involving cyclical events, and tackling more advanced mathematical concepts. This comprehensive guide will delve into the intricacies of finding the LCM of 3 and 8, exploring various methods and illustrating their practical applications. We'll go beyond a simple answer, uncovering the underlying principles and providing you with a robust understanding of this mathematical concept.
Understanding Least Common Multiples (LCMs)
Before we tackle the specific case of 3 and 8, let's establish a solid foundation in LCMs. The Least Common Multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. Think of it as the smallest number that contains all the numbers within the set as factors.
For example, the LCM of 2 and 3 is 6 because 6 is the smallest positive integer divisible by both 2 and 3. Similarly, the LCM of 4 and 6 is 12, as 12 is the smallest number divisible by both 4 and 6.
Methods for Finding the LCM of 3 and 8
Several methods can be employed to determine the LCM of 3 and 8. We'll explore three common approaches:
1. Listing Multiples
This method is intuitive and suitable for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
- Multiples of 8: 8, 16, 24, 32, 40...
Notice that the smallest multiple common to both lists is 24. Therefore, the LCM of 3 and 8 is 24.
2. Prime Factorization Method
This method is more efficient for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present.
- Prime factorization of 3: 3 (3 is a prime number)
- Prime factorization of 8: 2³ (8 = 2 x 2 x 2)
To find the LCM, we take the highest power of each prime factor present in either factorization:
- Highest power of 2: 2³ = 8
- Highest power of 3: 3¹ = 3
Multiply these together: 8 x 3 = 24. Therefore, the LCM of 3 and 8 is 24.
3. Using the Formula: LCM(a, b) = (|a x b|) / GCD(a, b)
This method utilizes the Greatest Common Divisor (GCD) of the two numbers. The GCD is the largest positive integer that divides both numbers without leaving a remainder. We can find the GCD using various methods, such as the Euclidean algorithm.
-
Finding the GCD of 3 and 8: The GCD of 3 and 8 is 1 because 1 is the only positive integer that divides both 3 and 8.
-
Applying the formula: LCM(3, 8) = (|3 x 8|) / GCD(3, 8) = 24 / 1 = 24
This confirms that the LCM of 3 and 8 is indeed 24.
Real-World Applications of LCM
The concept of LCM extends beyond theoretical mathematics; it finds practical applications in various real-world scenarios:
1. Scheduling and Synchronization
Imagine two machines operating on a cycle. Machine A completes a task every 3 minutes, while Machine B completes a task every 8 minutes. To find when both machines will complete a task simultaneously, we need to find the LCM of 3 and 8. The LCM, 24, indicates that both machines will complete a task together every 24 minutes.
2. Fraction Addition and Subtraction
When adding or subtracting fractions with different denominators, finding the LCM of the denominators is crucial for finding a common denominator. This allows us to perform the addition or subtraction effectively.
For example, adding 1/3 and 1/8 requires finding the LCM of 3 and 8, which is 24. We then rewrite the fractions with a common denominator of 24: (8/24) + (3/24) = 11/24.
3. Cyclical Events
Many real-world events follow cyclical patterns. For instance, consider two events that occur periodically. Finding the LCM helps determine when both events will coincide. This has applications in various fields, including astronomy, scheduling, and engineering.
Expanding the Concept: LCM of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For the prime factorization method, we simply consider the prime factors of all the numbers involved and take the highest power of each. For the listing method, we list multiples of all the numbers until we find the smallest common multiple. The formula method becomes more complex when dealing with more than two numbers but remains conceptually similar.
Conclusion: Mastering the LCM of 3 and 8 and Beyond
Understanding the Least Common Multiple, as exemplified by our exploration of the LCM of 3 and 8, is a cornerstone of mathematical proficiency. This comprehensive guide has equipped you not only with the answer (24) but also with the understanding of the underlying principles and various methods for calculating LCMs. The ability to calculate LCMs is a valuable skill applicable to numerous real-world situations, from scheduling tasks to simplifying complex fractions. By mastering this concept, you're better prepared to tackle more advanced mathematical problems and real-world challenges. Remember that the key lies in understanding the underlying principles, choosing the most appropriate method for the given numbers, and appreciating the versatility of this fundamental mathematical concept. The journey from simply knowing the LCM of 3 and 8 to understanding its broader implications is a significant step in your mathematical development.
Latest Posts
Latest Posts
-
Difference Between Meiosis 1 And Meiosis 2
Apr 02, 2025
-
Equation Of Circle In Parametric Form
Apr 02, 2025
-
How To Find The Complement Of An Angle
Apr 02, 2025
-
Nice Word That Starts With E
Apr 02, 2025
-
200 Inches Is How Many Feet
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Least Common Multiple 3 And 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
