What Is The Lcm Of 9 15
Juapaving
Apr 06, 2025 · 5 min read
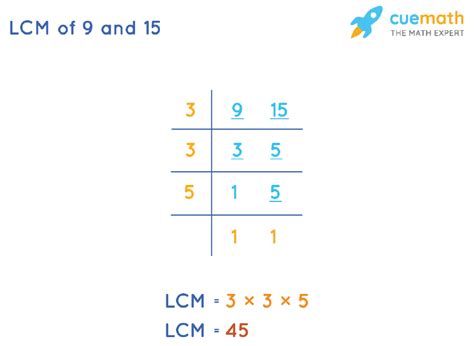
Table of Contents
What is the LCM of 9 and 15? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic problem, but understanding the underlying concepts and different methods for solving it is crucial for various mathematical applications, particularly in algebra, number theory, and even programming. This comprehensive guide will explore what the LCM of 9 and 15 is, delve into the various methods for calculating LCMs, and provide a broader understanding of the concept itself.
Understanding Least Common Multiples (LCM)
Before we tackle the specific LCM of 9 and 15, let's establish a solid foundation. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. Think of it as the smallest number that contains all the numbers as factors.
For example, consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12, 14, 16... and multiples of 3 are 3, 6, 9, 12, 15, 18... The common multiples are 6, 12, 18, and so on. The least common multiple is 6.
Methods for Calculating the LCM
Several methods can efficiently determine the LCM of two or more numbers. Let's examine the most common ones, applying them to find the LCM of 9 and 15:
1. Listing Multiples Method
This is the most straightforward method, especially for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72...
- Multiples of 15: 15, 30, 45, 60, 75, 90...
The smallest number that appears in both lists is 45. Therefore, the LCM(9, 15) = 45.
This method is simple but becomes cumbersome for larger numbers.
2. Prime Factorization Method
This method is more efficient, particularly for larger numbers. It involves breaking down each number into its prime factors.
- Prime factorization of 9: 3 x 3 = 3²
- Prime factorization of 15: 3 x 5
To find the LCM, we take the highest power of each prime factor present in either factorization and multiply them together.
In this case, the prime factors are 3 and 5. The highest power of 3 is 3² (from the factorization of 9), and the highest power of 5 is 5¹ (from the factorization of 15).
Therefore, LCM(9, 15) = 3² x 5 = 9 x 5 = 45.
This method is generally preferred for its efficiency and applicability to larger numbers.
3. Greatest Common Divisor (GCD) Method
This method uses the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The formula connecting LCM and GCD is:
LCM(a, b) x GCD(a, b) = a x b
First, we need to find the GCD of 9 and 15. We can use the Euclidean algorithm for this:
- Divide the larger number (15) by the smaller number (9): 15 ÷ 9 = 1 with a remainder of 6.
- Replace the larger number with the smaller number (9) and the smaller number with the remainder (6): 9 ÷ 6 = 1 with a remainder of 3.
- Repeat: 6 ÷ 3 = 2 with a remainder of 0.
- The GCD is the last non-zero remainder, which is 3.
Now, using the formula:
LCM(9, 15) x GCD(9, 15) = 9 x 15 LCM(9, 15) x 3 = 135 LCM(9, 15) = 135 ÷ 3 = 45
This method is also efficient and provides a deeper understanding of the relationship between LCM and GCD.
Applications of LCM
Understanding LCMs is vital in numerous mathematical and real-world scenarios:
-
Fraction Addition and Subtraction: Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators.
-
Scheduling Problems: Determining when events will occur simultaneously (e.g., buses arriving at a stop, machines completing cycles) often involves calculating the LCM of their respective periods.
-
Modular Arithmetic: LCMs play a crucial role in solving congruence problems in modular arithmetic.
-
Music Theory: LCMs help determine the least common period of musical rhythms.
-
Computer Science: LCM calculations are used in various algorithms and data structures.
Extending the Concept: LCM of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For the prime factorization method, we consider all the prime factors of all the numbers and take the highest power of each. For the GCD method, we can apply it iteratively. For instance, to find the LCM of 3, 6, and 9:
- Prime Factorization:
- 3 = 3
- 6 = 2 x 3
- 9 = 3 x 3 = 3²
The highest powers are 2¹, 3². Therefore, LCM(3, 6, 9) = 2 x 3² = 18.
- Iterative GCD Method: First, find the LCM of 3 and 6 (which is 6). Then, find the LCM of 6 and 9 (using any of the methods; the prime factorization method is easiest here, yielding 18).
Conclusion: The LCM of 9 and 15 is 45
We've explored several methods to determine the least common multiple of 9 and 15, arriving at the definitive answer: 45. Understanding the different approaches allows for flexibility in tackling LCM problems of varying complexity. The significance of LCM extends far beyond simple arithmetic; it forms a crucial foundation for advanced mathematical concepts and real-world applications. Mastering the calculation and comprehension of LCMs equips you with a valuable tool for problem-solving across numerous fields. Remember to choose the method that best suits the numbers involved for efficient calculation. The prime factorization method is generally preferred for its efficiency and broader applicability.
Latest Posts
Latest Posts
-
Difference Between A Square And A Rhombus
Apr 07, 2025
-
Capacity Of Doing Work Is Called
Apr 07, 2025
-
Is Ascending Order A To Z
Apr 07, 2025
-
Which Number Is A Factor Of 51
Apr 07, 2025
-
Finding The Area Under The Curve Calculator
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 9 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
