What Is The Lcm Of 7 21
Juapaving
Mar 28, 2025 · 5 min read
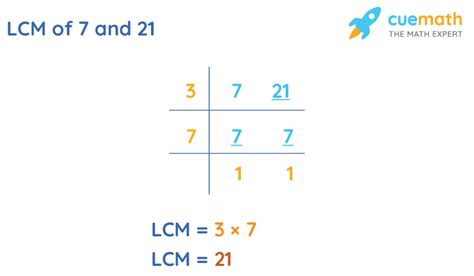
Table of Contents
What is the LCM of 7 and 21? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly in arithmetic and number theory. It has practical applications in various fields, from scheduling tasks to simplifying fractions. This article will thoroughly explore the concept of LCM, focusing specifically on finding the LCM of 7 and 21. We'll delve into different methods for calculating the LCM, explore the underlying mathematical principles, and provide a comprehensive understanding of this important topic.
Understanding Least Common Multiples (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the integers as factors. For example, the LCM of 2 and 3 is 6 because 6 is the smallest positive integer that is divisible by both 2 and 3.
Understanding the LCM is crucial for various mathematical operations, including:
- Simplifying fractions: Finding the LCM of the denominators helps in adding or subtracting fractions with different denominators.
- Solving problems involving ratios and proportions: LCM helps in finding equivalent ratios and proportions.
- Scheduling tasks: Determining when events will occur simultaneously often involves finding the LCM of the time intervals involved.
- Modular arithmetic: LCM plays a vital role in solving problems related to congruences and modular arithmetic.
Methods for Calculating the LCM
There are several effective methods to calculate the LCM of two or more numbers. Let's examine the most common approaches:
1. Listing Multiples Method
This is a straightforward method, especially suitable for smaller numbers. You list the multiples of each number until you find the smallest multiple that is common to both.
Let's find the LCM of 7 and 21 using this method:
- Multiples of 7: 7, 14, 21, 28, 35, ...
- Multiples of 21: 21, 42, 63, ...
The smallest multiple that appears in both lists is 21. Therefore, the LCM of 7 and 21 is 21.
This method is simple for small numbers but becomes less efficient as the numbers get larger.
2. Prime Factorization Method
This method utilizes the prime factorization of the numbers. It's particularly efficient for larger numbers. The steps are as follows:
-
Find the prime factorization of each number:
- 7 = 7 (7 is a prime number)
- 21 = 3 x 7
-
Identify the highest power of each prime factor present in the factorizations:
- The prime factors are 3 and 7.
- The highest power of 3 is 3¹ = 3.
- The highest power of 7 is 7¹.
-
Multiply the highest powers of all prime factors together:
- LCM(7, 21) = 3 x 7 = 21
This method provides a systematic and efficient way to calculate the LCM, regardless of the size of the numbers.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (Greatest Common Divisor) of two numbers are related through the following formula:
LCM(a, b) = (a x b) / GCD(a, b)
First, we need to find the GCD of 7 and 21. The GCD is the largest number that divides both 7 and 21 without leaving a remainder. In this case, the GCD(7, 21) = 7.
Now, we can use the formula:
LCM(7, 21) = (7 x 21) / 7 = 21
This method is efficient, especially when dealing with larger numbers where finding the GCD using the Euclidean algorithm is advantageous.
Why is the LCM of 7 and 21 equal to 21? A Deeper Look
The result, LCM(7, 21) = 21, is not accidental. It highlights a specific relationship between the two numbers. 21 is a multiple of 7 (21 = 7 x 3). This means that any multiple of 21 is also a multiple of 7. Consequently, the smallest multiple common to both 7 and 21 is simply 21 itself.
This illustrates an important principle: if one number is a multiple of the other, the LCM is the larger number.
Applications of LCM: Real-World Examples
The concept of LCM extends beyond abstract mathematical exercises. Here are some practical examples:
-
Scheduling Bus Routes: Two bus routes operate on a circular route. Bus A completes its route every 7 minutes, while Bus B completes its route every 21 minutes. To determine when both buses will be at the starting point simultaneously, we need to find the LCM(7, 21) = 21. Both buses will be at the starting point every 21 minutes.
-
Manufacturing Processes: A factory produces two types of products. Product X requires a machine cycle of 7 minutes, while Product Y requires a machine cycle of 21 minutes. To find the shortest time interval when both machines complete a cycle simultaneously, we find the LCM(7, 21) = 21 minutes. Production scheduling can be optimized based on this.
-
Music Synchronization: Two musical instruments play notes with frequencies of 7 Hz and 21 Hz. The LCM helps determine when both instruments will produce the same frequency simultaneously. This is crucial for harmonious musical arrangements.
Advanced Concepts and Extensions
While this article focuses on finding the LCM of 7 and 21, the concept extends to more than two numbers. For example, finding the LCM of 7, 21, and 35 requires similar methods, but the process becomes more involved. The prime factorization method remains a powerful tool for such calculations.
Furthermore, the concept of LCM extends to other mathematical structures, such as polynomials. Finding the LCM of polynomials involves similar principles, using factorization techniques specific to polynomials.
Conclusion: Mastering the LCM
Understanding and calculating the least common multiple is a crucial skill in mathematics with various practical applications. Whether using the listing multiples method, the prime factorization method, or the GCD method, mastering the LCM calculation is essential for problem-solving in numerous fields. This article provides a comprehensive understanding of the LCM concept, focusing specifically on the LCM of 7 and 21, and demonstrating its practical relevance in real-world scenarios. Remember, the key is to choose the most efficient method based on the numbers involved and your comfort level with the different approaches. By understanding the underlying principles, you'll be well-equipped to tackle more complex LCM problems in the future.
Latest Posts
Latest Posts
-
Nouns That Start With A G
Mar 31, 2025
-
How Much Atp Does Glycolysis Make
Mar 31, 2025
-
What Is The Lcm Of 3 5 11
Mar 31, 2025
-
What Is Difference Between Cilia And Flagella
Mar 31, 2025
-
A Horizontal Row In The Periodic Table Is Called
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 7 21 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
