What Is The Lcm Of 3 5 11
Juapaving
Mar 31, 2025 · 6 min read
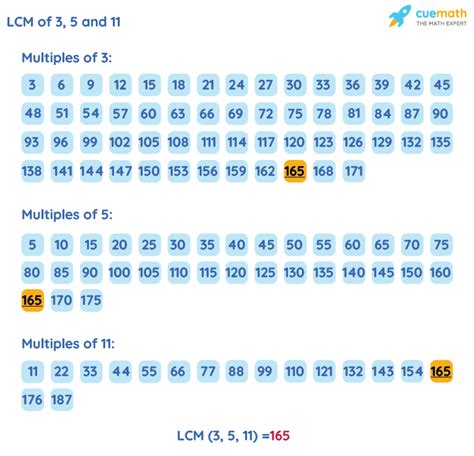
Table of Contents
Unveiling the LCM: A Deep Dive into the Least Common Multiple of 3, 5, and 11
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and exploring different methods can reveal a surprisingly rich mathematical landscape. This article delves into the calculation of the LCM of 3, 5, and 11, exploring various approaches, highlighting their practical applications, and connecting them to broader mathematical ideas. We'll move beyond a simple answer and explore the why behind the calculations, making this more than just a quick solution, but a journey into the heart of number theory.
What is the Least Common Multiple (LCM)?
Before we jump into finding the LCM of 3, 5, and 11, let's establish a clear understanding of what an LCM is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that contains all the given numbers as factors.
Think of it like finding the smallest common denominator when adding or subtracting fractions. The LCM is crucial for simplifying fractions and performing various arithmetic operations smoothly.
Method 1: Prime Factorization – The Foundation of LCM Calculation
This method is arguably the most fundamental and conceptually insightful way to determine the LCM. It leverages the prime factorization of each number, revealing the building blocks of their multiplicative structure.
-
Prime Factorization: First, we express each number as a product of its prime factors. Prime numbers are numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.).
- 3 = 3 (3 is already a prime number)
- 5 = 5 (5 is already a prime number)
- 11 = 11 (11 is already a prime number)
-
Identifying the Highest Powers: Next, we identify the highest power of each prime factor present in the factorizations. In this case, we have only three distinct prime factors: 3, 5, and 11. Each appears only once and raised to the power of 1.
-
Calculating the LCM: To find the LCM, we multiply the highest powers of all the prime factors together.
LCM(3, 5, 11) = 3¹ * 5¹ * 11¹ = 3 * 5 * 11 = 165
Therefore, the least common multiple of 3, 5, and 11 is $\boxed{165}$.
Method 2: Listing Multiples – A More Intuitive Approach (Suitable for Smaller Numbers)
This method is straightforward and easily understood, particularly when dealing with smaller numbers. It involves listing the multiples of each number until a common multiple is found.
-
Listing Multiples: We list the multiples of each number:
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99, 102, 105, 108, 111, 114, 117, 120, 123, 126, 129, 132, 135, 138, 141, 144, 147, 150, 153, 156, 159, 162, 165...
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100, 105, 110, 115, 120, 125, 130, 135, 140, 145, 150, 155, 165...
- Multiples of 11: 11, 22, 33, 44, 55, 66, 77, 88, 99, 110, 121, 132, 143, 154, 165...
-
Identifying the Smallest Common Multiple: The smallest number that appears in all three lists is 165.
Therefore, the LCM(3, 5, 11) = 165. This method is less efficient for larger numbers but provides a clear visual representation of the concept.
Method 3: Using the Formula (for Two Numbers) and Iterative Application
While there isn't a direct formula for finding the LCM of three or more numbers simultaneously, we can use the formula for two numbers iteratively. The formula for the LCM of two numbers a and b is:
LCM(a, b) = (|a * b|) / GCD(a, b)
where GCD(a, b) is the greatest common divisor of a and b.
-
Find LCM(3, 5):
GCD(3, 5) = 1 (since 3 and 5 are coprime – they share no common factors other than 1) LCM(3, 5) = (3 * 5) / 1 = 15
-
Find LCM(15, 11):
GCD(15, 11) = 1 (15 and 11 are coprime) LCM(15, 11) = (15 * 11) / 1 = 165
Therefore, the LCM(3, 5, 11) = 165. This method demonstrates how the LCM concept builds upon the GCD and shows a step-by-step approach.
The Significance of LCM in Real-World Applications
The seemingly abstract concept of the least common multiple finds practical applications in various fields:
-
Scheduling: Imagine you have three different events occurring at different intervals. Event A happens every 3 days, Event B every 5 days, and Event C every 11 days. To find when all three events will coincide, you need to find the LCM(3, 5, 11) = 165. All three events will happen together every 165 days.
-
Fractions: When adding or subtracting fractions, finding the LCM of the denominators is crucial for finding a common denominator and simplifying the calculation.
-
Gear Ratios: In mechanics, gear ratios and rotational speeds often involve finding the LCM to determine when gears will be synchronized or when certain events will align in a machine's operation.
-
Cyclic Processes: In many scientific and engineering contexts, processes repeat cyclically. Finding the LCM helps determine when cycles will coincide or synchronize.
-
Music Theory: Rhythmic patterns in music often involve finding the LCM to determine when different rhythmic patterns align.
Extending the Concept: LCM of More Than Three Numbers
The methods described above can be extended to find the LCM of more than three numbers. The prime factorization method remains the most robust approach, while the iterative method using the formula for two numbers can be applied sequentially.
For example, to find the LCM of 3, 5, 11, and 7:
- Prime Factorization: 3 = 3, 5 = 5, 11 = 11, 7 = 7
- Highest Powers: The highest power of each prime factor is 3¹, 5¹, 7¹, and 11¹.
- LCM: LCM(3, 5, 11, 7) = 3 * 5 * 7 * 11 = 1155
Conclusion: Beyond the Calculation – Understanding the Mathematical Significance
This in-depth exploration of finding the LCM of 3, 5, and 11 transcends a simple arithmetic problem. It highlights the fundamental importance of prime factorization, demonstrates various computational approaches, and underscores the practical applications of this seemingly abstract mathematical concept across various disciplines. Understanding LCM isn't just about getting the answer; it's about grasping the underlying principles of number theory and appreciating its relevance in the real world. By mastering this concept, you unlock a deeper understanding of the interconnectedness of mathematics and its power to solve real-world problems.
Latest Posts
Latest Posts
-
When Heating A Liquid In A Test Tube You Should
Apr 01, 2025
-
How Many Bones Do Shark Have
Apr 01, 2025
-
Least Common Multiple 12 And 18
Apr 01, 2025
-
What Phase Is The Reverse Of Prophase
Apr 01, 2025
-
Is Tungsten A Metal Or Nonmetal
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 3 5 11 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
