What Is The Lcm Of 5 And 12
Juapaving
Apr 05, 2025 · 5 min read
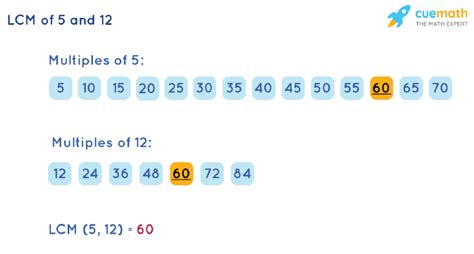
Table of Contents
What is the LCM of 5 and 12? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) is a fundamental concept in mathematics, crucial for various applications from simplifying fractions to solving complex algebraic equations. This article provides a comprehensive exploration of how to find the LCM of 5 and 12, explaining the process in detail and highlighting different methods. We will also delve into the underlying mathematical principles and showcase practical examples to solidify your understanding.
Understanding Least Common Multiples (LCM)
Before tackling the LCM of 5 and 12 specifically, let's define what a least common multiple actually is. The LCM of two or more integers is the smallest positive integer that is divisible by all the given integers without leaving a remainder. Think of it as the smallest number that contains all the original numbers as factors.
For example, let's consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12, 14... and multiples of 3 are 3, 6, 9, 12, 15... The smallest number that appears in both lists is 6. Therefore, the LCM of 2 and 3 is 6.
Method 1: Listing Multiples
One straightforward method to find the LCM is by listing the multiples of each number until you find the smallest common multiple. Let's apply this to 5 and 12:
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, ...
- Multiples of 12: 12, 24, 36, 48, 60, 72, ...
Notice that the smallest number that appears in both lists is 60. Therefore, the LCM of 5 and 12 is 60. This method works well for smaller numbers, but it becomes less efficient when dealing with larger numbers.
Method 2: Prime Factorization
A more efficient and mathematically elegant approach involves prime factorization. This method breaks down each number into its prime factors – numbers that are only divisible by 1 and themselves.
- Prime factorization of 5: 5 (5 is a prime number)
- Prime factorization of 12: 2 x 2 x 3 = 2² x 3
To find the LCM using prime factorization, we follow these steps:
- Identify the prime factors of each number. As shown above, 5 has only one prime factor (5), and 12 has two prime factors (2 and 3).
- Find the highest power of each prime factor present in the factorizations. The highest power of 2 is 2², the highest power of 3 is 3¹, and the highest power of 5 is 5¹.
- Multiply the highest powers together. LCM(5, 12) = 2² x 3 x 5 = 4 x 3 x 5 = 60
This method is particularly useful for larger numbers, as it avoids the tedious process of listing out multiples. It provides a systematic and reliable way to calculate the LCM.
Method 3: Using the Formula (LCM and GCD Relationship)
There's a powerful relationship between the least common multiple (LCM) and the greatest common divisor (GCD) of two numbers. The formula is:
LCM(a, b) x GCD(a, b) = a x b
Where 'a' and 'b' are the two numbers. This means that if we know the GCD, we can easily calculate the LCM.
Let's find the GCD of 5 and 12 using the Euclidean algorithm:
- Divide the larger number (12) by the smaller number (5): 12 ÷ 5 = 2 with a remainder of 2.
- Replace the larger number with the smaller number (5) and the smaller number with the remainder (2).
- Repeat: 5 ÷ 2 = 2 with a remainder of 1.
- Repeat: 2 ÷ 1 = 2 with a remainder of 0. The GCD is the last non-zero remainder, which is 1.
Therefore, GCD(5, 12) = 1. Now, we can use the formula:
LCM(5, 12) = (5 x 12) / GCD(5, 12) = 60 / 1 = 60
This method showcases the interconnectedness of GCD and LCM, providing an alternative and efficient way to calculate the LCM. It's especially beneficial when dealing with numbers where prime factorization might be more complex.
Applications of LCM
Understanding and calculating the LCM has numerous applications across various mathematical fields and real-world scenarios:
- Fraction Addition and Subtraction: Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators.
- Scheduling Problems: Determining when events will occur simultaneously, such as the alignment of planetary orbits or scheduling recurring tasks. For example, two machines operate at different intervals; the LCM helps determine when they will operate simultaneously again.
- Modular Arithmetic: LCM plays a crucial role in solving problems related to congruences and modular arithmetic.
- Music Theory: Determining the least common multiple of rhythmic patterns to understand when they will coincide.
- Pattern Recognition: Identifying repeating patterns and cycles in various contexts.
Working with Larger Numbers
The methods described above are adaptable to larger numbers. Let's consider finding the LCM of 24 and 36:
Method 1 (Listing Multiples): This method becomes less practical with larger numbers.
Method 2 (Prime Factorization):
- Prime factorization of 24: 2³ x 3
- Prime factorization of 36: 2² x 3²
LCM(24, 36) = 2³ x 3² = 8 x 9 = 72
Method 3 (Using GCD):
First, find the GCD of 24 and 36 using the Euclidean algorithm:
- 36 ÷ 24 = 1 remainder 12
- 24 ÷ 12 = 2 remainder 0
GCD(24, 36) = 12
Now, use the formula:
LCM(24, 36) = (24 x 36) / GCD(24, 36) = 864 / 12 = 72
Conclusion: Mastering LCM Calculations
This in-depth exploration of the least common multiple, focusing specifically on the LCM of 5 and 12, has demonstrated various methods for calculating it. While the simple listing method works well for smaller numbers, prime factorization and the LCM-GCD relationship provide more efficient and powerful approaches for larger integers. Understanding these methods empowers you to tackle LCM calculations confidently, paving the way for a deeper understanding of numerous mathematical concepts and their practical applications. Remember to choose the method that best suits the numbers involved and your comfort level with different mathematical techniques. Practice is key to mastering LCM calculations and appreciating their significance in diverse areas of mathematics and beyond.
Latest Posts
Latest Posts
-
How Much Is 70 Cm In Inches
Apr 05, 2025
-
Benedicts Reagent Is Used To Identify Which Of The Following
Apr 05, 2025
-
What Is A Positively Charged Ion Called
Apr 05, 2025
-
Is Iron Rust A Chemical Change
Apr 05, 2025
-
Five Letter Words Starting With Ri
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 5 And 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
