What Is The Lcm Of 26 And 39
Juapaving
Apr 01, 2025 · 5 min read
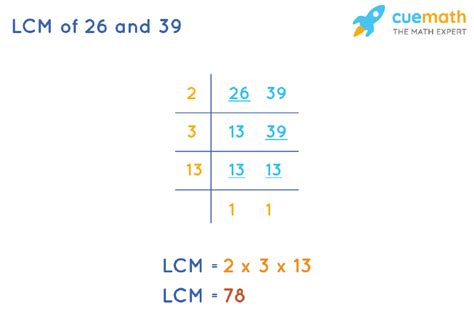
Table of Contents
What is the LCM of 26 and 39? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and exploring different methods can significantly improve your mathematical skills and problem-solving abilities. This comprehensive guide delves into the LCM of 26 and 39, providing a detailed explanation, exploring various calculation methods, and highlighting the importance of LCM in real-world applications. We’ll also look at how this seemingly simple calculation connects to broader mathematical concepts.
Understanding Least Common Multiples (LCM)
Before we tackle the LCM of 26 and 39, let's establish a solid foundation. The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the given integers. Think of it as the smallest number that contains all the given numbers as factors.
For example, the LCM of 2 and 3 is 6 because 6 is the smallest positive integer divisible by both 2 and 3. Similarly, the LCM of 4 and 6 is 12, as 12 is the smallest number divisible by both 4 and 6.
Method 1: Prime Factorization Method
This is arguably the most fundamental and widely used method for finding the LCM. It involves breaking down each number into its prime factors. Prime factorization is the process of expressing a number as a product of its prime numbers (numbers divisible only by 1 and themselves).
Let's apply this to find the LCM of 26 and 39:
1. Prime Factorization of 26:
26 = 2 x 13
2. Prime Factorization of 39:
39 = 3 x 13
3. Identifying Common and Unique Prime Factors:
Both 26 and 39 share the prime factor 13. The unique prime factors are 2 and 3.
4. Calculating the LCM:
To find the LCM, we multiply the highest power of each prime factor present in either factorization:
LCM(26, 39) = 2 x 3 x 13 = 78
Therefore, the least common multiple of 26 and 39 is 78.
Method 2: Listing Multiples Method
This method involves listing the multiples of each number until you find the smallest multiple common to both. While simple for smaller numbers, it becomes less efficient for larger numbers.
1. List Multiples of 26:
26, 52, 78, 104, 130, 156, ...
2. List Multiples of 39:
39, 78, 117, 156, ...
3. Identify the Smallest Common Multiple:
The smallest multiple that appears in both lists is 78.
Therefore, the LCM of 26 and 39 is 78.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (greatest common divisor) of two numbers are closely related. The product of the LCM and GCD of two numbers is equal to the product of the two numbers. This relationship provides an alternative method for calculating the LCM.
1. Find the GCD of 26 and 39:
We can use the Euclidean algorithm to find the GCD.
- Divide 39 by 26: 39 = 26 x 1 + 13
- Divide 26 by 13: 26 = 13 x 2 + 0
The last non-zero remainder is the GCD, which is 13.
2. Calculate the LCM using the GCD:
LCM(26, 39) = (26 x 39) / GCD(26, 39) = (26 x 39) / 13 = 78
Therefore, the LCM of 26 and 39 is 78.
Real-World Applications of LCM
The concept of LCM isn't just confined to textbooks; it has practical applications in various fields:
-
Scheduling: Imagine two buses depart from the same station, one every 26 minutes and the other every 39 minutes. The LCM (78 minutes) determines when both buses will depart simultaneously again.
-
Project Management: If a project requires two tasks to be completed, one taking 26 days and the other 39 days, the LCM helps determine the shortest time to complete both tasks, assuming they can run concurrently.
-
Music: LCM is crucial in music theory for calculating the least common denominator of different rhythmic patterns, ensuring synchronization and harmony.
-
Construction: In construction, LCM can be useful for calculating the least common length for cutting materials efficiently, avoiding waste.
Expanding the Concept: LCM of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For the prime factorization method, you simply consider all prime factors from all numbers, taking the highest power of each. For the GCD method, you can extend the Euclidean algorithm or use other techniques to find the GCD of multiple numbers.
Beyond the Numbers: Exploring Mathematical Connections
Understanding the LCM is a stepping stone to more advanced mathematical concepts. It’s intrinsically linked to:
-
Modular Arithmetic: LCM plays a critical role in solving congruence equations, a key component of number theory.
-
Abstract Algebra: The concept of LCM extends to more abstract algebraic structures like rings and modules.
Conclusion: Mastering the LCM
Calculating the LCM of 26 and 39, as illustrated above, might seem trivial. However, grasping the underlying principles and exploring different calculation methods provides a deeper understanding of fundamental mathematical concepts. This understanding is crucial not just for academic purposes but also for solving real-world problems across various disciplines. The ability to efficiently determine the LCM, along with a comprehension of its underlying connections to other mathematical areas, is a valuable asset in many fields. Remember to practice using different methods to solidify your understanding and choose the most efficient approach based on the numbers involved.
Latest Posts
Latest Posts
-
Is Boiling A Physical Or Chemical Change
Apr 02, 2025
-
Rectangle Has How Many Lines Of Symmetry
Apr 02, 2025
-
How To Find Recoil In Physics
Apr 02, 2025
-
87 Inches Is How Many Feet
Apr 02, 2025
-
Electrons Are Lost Or Gained During
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 26 And 39 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
