What Is The Factors Of 100
Juapaving
Mar 26, 2025 · 5 min read
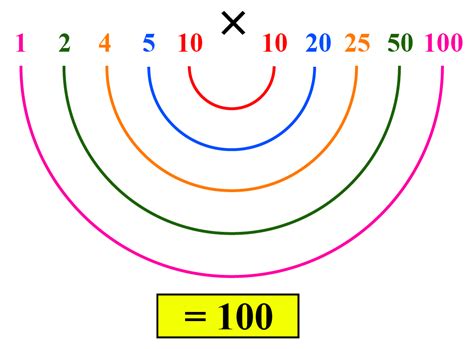
Table of Contents
What are the Factors of 100? A Deep Dive into Number Theory
Finding the factors of a number might seem like a simple arithmetic exercise, but understanding the concept unlocks a deeper appreciation of number theory and its applications in various fields. This comprehensive guide delves into the factors of 100, exploring the underlying mathematical principles and showcasing the practical relevance of factorization.
Understanding Factors and Divisors
Before we embark on identifying the factors of 100, let's establish a clear understanding of the terminology. A factor, also known as a divisor, of a number is a whole number that divides the number exactly without leaving a remainder. In simpler terms, if you divide a number by its factor, the result is a whole number.
For example, the factors of 12 are 1, 2, 3, 4, 6, and 12 because each of these numbers divides 12 without leaving any remainder.
Finding the Factors of 100: A Step-by-Step Approach
There are several ways to find the factors of 100. Let's explore the most common methods:
Method 1: Systematic Division
This method involves systematically dividing 100 by each whole number, starting from 1, and checking if the result is a whole number.
- Divide by 1: 100 ÷ 1 = 100. Therefore, 1 and 100 are factors.
- Divide by 2: 100 ÷ 2 = 50. Therefore, 2 and 50 are factors.
- Divide by 3: 100 ÷ 3 = 33 with a remainder. 3 is not a factor.
- Divide by 4: 100 ÷ 4 = 25. Therefore, 4 and 25 are factors.
- Divide by 5: 100 ÷ 5 = 20. Therefore, 5 and 20 are factors.
- Divide by 6: 100 ÷ 6 = 16 with a remainder. 6 is not a factor.
- Divide by 7: 100 ÷ 7 = 14 with a remainder. 7 is not a factor.
- Divide by 8: 100 ÷ 8 = 12 with a remainder. 8 is not a factor.
- Divide by 9: 100 ÷ 9 = 11 with a remainder. 9 is not a factor.
- Divide by 10: 100 ÷ 10 = 10. Therefore, 10 and 10 are factors.
Notice that after reaching 10, we've essentially found all the factors. Any higher number we try will already have been identified as a factor in a previous step.
Method 2: Prime Factorization
This method is more efficient for larger numbers. It involves breaking down the number into its prime factors – numbers that are only divisible by 1 and themselves.
-
Find the prime factors of 100: We can express 100 as 10 x 10. Since 10 = 2 x 5, we can rewrite 100 as 2 x 5 x 2 x 5, or 2² x 5².
-
Generate the factors: To find all the factors, we consider all possible combinations of the prime factors:
- 2⁰ x 5⁰ = 1
- 2¹ x 5⁰ = 2
- 2² x 5⁰ = 4
- 2⁰ x 5¹ = 5
- 2¹ x 5¹ = 10
- 2² x 5¹ = 20
- 2⁰ x 5² = 25
- 2¹ x 5² = 50
- 2² x 5² = 100
This method systematically generates all factors without any omissions.
The Complete List of Factors of 100
Using either method, we arrive at the following list of factors for 100: 1, 2, 4, 5, 10, 20, 25, 50, and 100.
Applications of Factorization
Understanding factors and factorization is crucial in various mathematical and real-world applications:
1. Simplifying Fractions:
Finding the greatest common factor (GCF) of the numerator and denominator allows us to simplify fractions to their lowest terms. For example, simplifying the fraction 50/100 requires finding the GCF (50) and dividing both the numerator and denominator by it, resulting in the simplified fraction 1/2.
2. Solving Equations:
Factorization is a fundamental technique in solving polynomial equations. Finding the factors of a polynomial allows us to determine its roots (or zeros), which are the values of the variable that make the polynomial equal to zero.
3. Cryptography:
Factorization plays a significant role in modern cryptography, particularly in public-key cryptosystems like RSA. The security of these systems relies on the difficulty of factoring large composite numbers into their prime factors.
4. Geometry and Measurement:
Factors are essential in solving problems related to area, volume, and other geometric measurements. For instance, determining the possible dimensions of a rectangle with a specific area involves finding the factors of that area.
5. Data Analysis and Statistics:
Factor analysis is a statistical method used to identify underlying factors or variables that explain the correlations among a set of observed variables. This technique is widely used in social sciences, psychology, and market research.
Beyond the Basics: Exploring Divisibility Rules
Knowing divisibility rules can expedite the process of finding factors. These rules provide quick ways to determine if a number is divisible by a certain factor without performing the actual division.
- Divisibility by 2: A number is divisible by 2 if it's an even number (ends in 0, 2, 4, 6, or 8).
- Divisibility by 3: A number is divisible by 3 if the sum of its digits is divisible by 3.
- Divisibility by 4: A number is divisible by 4 if the last two digits are divisible by 4.
- Divisibility by 5: A number is divisible by 5 if it ends in 0 or 5.
- Divisibility by 6: A number is divisible by 6 if it's divisible by both 2 and 3.
- Divisibility by 9: A number is divisible by 9 if the sum of its digits is divisible by 9.
- Divisibility by 10: A number is divisible by 10 if it ends in 0.
Applying these rules, we can quickly confirm that 100 is divisible by 1, 2, 4, 5, 10, 20, 25, 50, and 100.
Conclusion: The Significance of Factors
Understanding the factors of a number, especially a seemingly simple number like 100, opens doors to a deeper understanding of mathematical concepts. The methods for finding factors, from systematic division to prime factorization, are not merely arithmetic exercises but tools that underpin various advanced mathematical applications and real-world problem-solving. The seemingly basic concept of factorization has profound implications across diverse fields, reinforcing its importance in mathematical literacy and beyond. By mastering the techniques and understanding the significance of factors, one can significantly enhance their mathematical abilities and problem-solving skills.
Latest Posts
Latest Posts
-
Direction Of Propagation Of Electromagnetic Wave
Mar 29, 2025
-
Write 3 8 As A Percent
Mar 29, 2025
-
Which Quadrilaterals Have Diagonals That Bisect Opposite Angles
Mar 29, 2025
-
List All The Factors Of 15
Mar 29, 2025
-
Is The Square Root Of 72 Rational Or Irrational
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about What Is The Factors Of 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
