Which Quadrilaterals Have Diagonals That Bisect Opposite Angles
Juapaving
Mar 29, 2025 · 5 min read
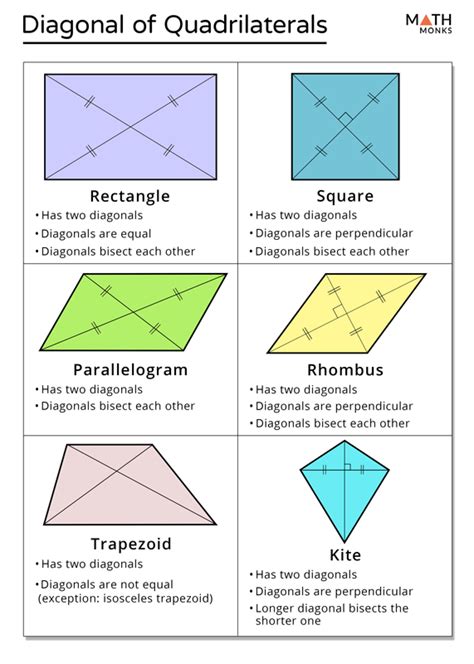
Table of Contents
Which Quadrilaterals Have Diagonals that Bisect Opposite Angles?
Understanding the properties of quadrilaterals is crucial in geometry. Among the many characteristics we can examine, the behavior of diagonals holds significant importance. This article delves deep into the fascinating world of quadrilaterals, focusing specifically on those whose diagonals bisect opposite angles. We will explore the defining characteristics, prove key theorems, and differentiate between quadrilaterals exhibiting this property.
Defining the Property: Diagonals Bisecting Opposite Angles
Before we delve into specific quadrilaterals, let's clarify the property we're investigating. A quadrilateral's diagonals bisect opposite angles if each diagonal divides two opposite angles into two congruent angles. In other words, if we have a quadrilateral ABCD, and diagonals AC and BD intersect at point E, then the diagonals bisect opposite angles if:
- ∠DAE ≅ ∠CAE
- ∠ABE ≅ ∠CBE
- ∠BCE ≅ ∠DCE
- ∠CDE ≅ ∠ADE
This seemingly simple property significantly narrows down the types of quadrilaterals we're considering. Not all quadrilaterals possess this characteristic. Let's investigate the quadrilaterals that do.
Rhombus: A Key Player
The rhombus, a quadrilateral with all four sides congruent, is a prime example. Let's prove that its diagonals bisect opposite angles.
Proof: Diagonals of a Rhombus Bisect Opposite Angles
-
Consider a rhombus ABCD. By definition, AB ≅ BC ≅ CD ≅ DA.
-
Draw diagonals AC and BD, intersecting at point E.
-
Focus on triangles ΔABE and ΔCBE. We know AB ≅ BC (sides of the rhombus). Also, AE ≅ CE (diagonals of a rhombus bisect each other). Finally, BE ≅ BE (reflexive property). Therefore, ΔABE ≅ ΔCBE by SSS (Side-Side-Side) congruence.
-
Congruent angles: Because ΔABE ≅ ΔCBE, we conclude that ∠ABE ≅ ∠CBE and ∠BAE ≅ ∠BCE. This shows that the diagonal BD bisects angles B and angles A.
-
Repeat the process: Applying a similar argument to triangles ΔADE and ΔCDE, we can prove that the diagonal AC bisects angles A and C.
Therefore, the diagonals of a rhombus bisect opposite angles. This proof highlights the inherent connection between the equal side lengths and the angle-bisecting diagonals.
Square: A Special Case of a Rhombus
A square, a quadrilateral with four right angles and four congruent sides, is a special case of a rhombus. Since a square is a rhombus, it automatically inherits the property of having diagonals that bisect opposite angles. In the case of a square, the diagonals also bisect each other at right angles. This adds another layer of geometric significance to the square's properties.
Kite: Another Contender
A kite is a quadrilateral with two pairs of adjacent congruent sides. Interestingly, the diagonals of a kite also bisect opposite angles, but only one pair of opposite angles.
Proof: Diagonals of a Kite Bisect Opposite Angles (Partially)
-
Consider a kite ABCD, with AB ≅ AD and BC ≅ CD.
-
Draw diagonals AC and BD, intersecting at point E.
-
Focus on triangles ΔABC and ΔADC. We know AB ≅ AD, BC ≅ DC (definition of a kite), and AC ≅ AC (reflexive property). Therefore, ΔABC ≅ ΔADC by SSS congruence.
-
Congruent angles: Since ΔABC ≅ ΔADC, we have ∠BAC ≅ ∠DAC and ∠BCA ≅ ∠DCA. This means that the diagonal AC bisects angles A and C.
However, the diagonal BD does not necessarily bisect angles B and D. Only one pair of opposite angles is bisected by the diagonals in a kite. This distinction separates it from the rhombus and square.
Differentiating Key Quadrilaterals
It's crucial to understand the nuances between these quadrilaterals. While rhombuses and squares have diagonals that bisect both pairs of opposite angles, kites only bisect one pair. This difference stems from their defining characteristics. A rhombus's equal sides force the diagonals to act as angle bisectors for all four angles. Kites, with only two pairs of adjacent sides congruent, lead to angle bisection only for the angles between the pairs of congruent sides.
| Quadrilateral | Diagonals Bisect Opposite Angles | Other Key Properties |
|---|---|---|
| Rhombus | Yes, both pairs | All sides congruent |
| Square | Yes, both pairs | All sides congruent, four right angles |
| Kite | Yes, one pair | Two pairs of adjacent congruent sides |
| Rectangle | No | Four right angles |
| Parallelogram | No (unless it's a rhombus) | Opposite sides are parallel and congruent |
| Trapezoid | No | One pair of parallel sides |
Implications and Applications
The property of diagonals bisecting opposite angles has significant implications in various geometric problems and applications:
- Area calculations: Knowing that diagonals bisect angles in a rhombus can simplify area calculations.
- Construction problems: Understanding this property can help in constructing certain geometric figures.
- Proofs and theorems: This property is often used as a step in proving more complex geometric theorems.
- Symmetry: The presence of angle-bisecting diagonals often indicates a certain type of symmetry within the quadrilateral.
Further Exploration
This in-depth analysis of quadrilaterals and their diagonals reveals the fascinating interplay between a shape's defining properties and the geometric consequences. Further exploration could involve examining how these properties relate to other concepts like area, perimeter, and circumcircles. Exploring more complex quadrilaterals and investigating similar properties in higher-dimensional shapes could lead to further mathematical discoveries. The beauty of geometry lies in its ability to reveal intricate relationships through seemingly simple observations, as demonstrated by the seemingly simple yet revealing property of diagonals bisecting opposite angles in specific quadrilaterals. Continued investigation in this area remains a fertile ground for mathematical exploration.
The study of quadrilaterals provides a rich foundation for understanding more advanced geometrical concepts. By analyzing the properties of diagonals and their relationship to the angles within the quadrilaterals, a deeper appreciation for the elegance and interconnectedness of geometric principles is achieved. This exploration also serves as a stepping stone for more complex mathematical investigations in the future. Remember, the key is to carefully examine the definitions and properties of each type of quadrilateral to fully grasp the behavior of its diagonals.
Latest Posts
Latest Posts
-
What Is The Lcm Of 2 3 And 6
Mar 31, 2025
-
What Ratio Is The Same As 2 3
Mar 31, 2025
-
The Role Of Hydrochloric Acid In Protein Digestion Is To
Mar 31, 2025
-
Is Dna Copied Before Meiosis 2
Mar 31, 2025
-
How Were The Mauryan And Gupta Empires Alike
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Which Quadrilaterals Have Diagonals That Bisect Opposite Angles . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
