15 4 As A Mixed Number
Juapaving
Apr 01, 2025 · 5 min read
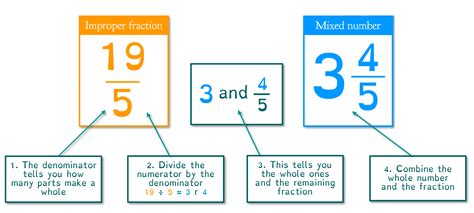
Table of Contents
15/4 as a Mixed Number: A Comprehensive Guide
Understanding fractions and how to convert them into mixed numbers is a fundamental skill in mathematics. This comprehensive guide will delve into the process of converting the improper fraction 15/4 into a mixed number, explaining the underlying concepts and providing practical examples to solidify your understanding. We'll also explore related concepts and offer tips for mastering fraction conversion.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 1 ½, 2 ¾, and 3 ⅛ are all mixed numbers. They represent a quantity larger than one whole unit.
Converting Improper Fractions to Mixed Numbers
An improper fraction is a fraction where the numerator is greater than or equal to the denominator. The fraction 15/4 is an improper fraction because the numerator (15) is larger than the denominator (4). To convert an improper fraction to a mixed number, you perform a division.
Steps to Convert 15/4 to a Mixed Number:
- Divide the numerator by the denominator: Divide 15 by 4.
- Determine the whole number: The quotient (the result of the division) becomes the whole number part of the mixed number. 15 divided by 4 is 3 with a remainder of 3. Therefore, the whole number is 3.
- Determine the fractional part: The remainder becomes the numerator of the fractional part of the mixed number. The denominator remains the same as the original fraction. In this case, the remainder is 3, so the fractional part is 3/4.
- Combine the whole number and the fractional part: Combine the whole number and the fractional part to form the mixed number. Therefore, 15/4 as a mixed number is 3 ¾.
Let's illustrate this with a visual representation:
Imagine you have 15 quarters. Since 4 quarters make a dollar, you can make 3 whole dollars (3 x 4 = 12 quarters) and have 3 quarters left over. This visually represents 3 ¾ dollars.
Practical Applications of Mixed Numbers
Mixed numbers are used frequently in everyday life and various fields:
- Cooking and Baking: Recipes often call for mixed number measurements, such as 2 ½ cups of flour or 1 ¾ teaspoons of baking powder.
- Construction and Engineering: Measurements in construction and engineering frequently involve mixed numbers to represent precise lengths or quantities.
- Data Analysis: In data analysis, mixed numbers might represent averages or proportions.
- Everyday Measurements: When measuring lengths, weights, or volumes, you may encounter mixed numbers.
Working with Mixed Numbers
Once you've converted an improper fraction to a mixed number, you can perform various mathematical operations:
- Addition and Subtraction: When adding or subtracting mixed numbers, it's often easier to convert them to improper fractions first, perform the operation, and then convert the result back to a mixed number if needed.
- Multiplication and Division: Multiplying and dividing mixed numbers usually involves converting them to improper fractions first to simplify the calculations.
Further Exploration: Other Improper Fraction Conversions
Let's practice converting a few more improper fractions to mixed numbers to solidify our understanding:
- 22/5: Dividing 22 by 5 gives a quotient of 4 and a remainder of 2. Therefore, 22/5 = 4 2/5.
- 17/3: Dividing 17 by 3 gives a quotient of 5 and a remainder of 2. Therefore, 17/3 = 5 ⅔.
- 25/8: Dividing 25 by 8 gives a quotient of 3 and a remainder of 1. Therefore, 25/8 = 3 ⅛.
Converting Mixed Numbers back to Improper Fractions
It's also essential to understand the reverse process: converting a mixed number back to an improper fraction. This is useful when performing calculations involving mixed numbers.
Steps to Convert a Mixed Number to an Improper Fraction:
- Multiply the whole number by the denominator: Multiply the whole number of the mixed number by the denominator of the fraction.
- Add the numerator: Add the result from step 1 to the numerator of the fraction.
- Keep the denominator: The denominator remains the same.
- Form the improper fraction: The result from step 2 becomes the numerator of the improper fraction, and the denominator remains unchanged.
Let's convert 3 ¾ back to an improper fraction:
- 3 (whole number) x 4 (denominator) = 12
- 12 + 3 (numerator) = 15
- The denominator remains 4.
- Therefore, 3 ¾ = 15/4.
Troubleshooting Common Mistakes
When converting fractions, some common mistakes can occur:
- Incorrect division: Ensure you accurately divide the numerator by the denominator.
- Misinterpreting the remainder: The remainder is crucial in determining the fractional part of the mixed number.
- Forgetting the denominator: Always maintain the original denominator when forming the mixed number or improper fraction.
Advanced Concepts and Practice
To further enhance your understanding, explore these advanced concepts:
- Simplifying fractions: Always simplify the fractional part of your mixed number to its lowest terms. For example, 6/8 should be simplified to ¾.
- Working with negative fractions: The principles remain the same when dealing with negative improper fractions; just remember to carry the negative sign throughout the conversion process.
- Comparing mixed numbers: Practice comparing the magnitude of mixed numbers.
By mastering the conversion between improper fractions and mixed numbers, you’ll significantly improve your mathematical skills and ability to solve various real-world problems. Remember to practice regularly and utilize visual aids to strengthen your understanding of these fundamental concepts. Consistent practice and a systematic approach will lead to proficiency in handling fractions and mixed numbers.
Latest Posts
Latest Posts
-
If 2 Matrix Multiplication Is 0
Apr 02, 2025
-
Find The Square Root Of 121
Apr 02, 2025
-
C In Terms Of Mu And Epsilon
Apr 02, 2025
-
Descriptive Words That Start With D
Apr 02, 2025
-
Chemical Formula For Magnesium And Iodine
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about 15 4 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
