What Is The Factor Of 59
Juapaving
Mar 27, 2025 · 5 min read
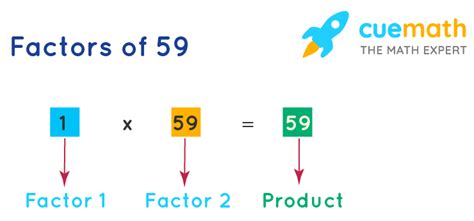
Table of Contents
What are the Factors of 59? A Deep Dive into Prime Numbers and Divisibility
The question, "What are the factors of 59?" might seem deceptively simple. However, understanding the answer unlocks a deeper appreciation for prime numbers, divisibility rules, and fundamental concepts in number theory. Let's embark on a comprehensive exploration of this seemingly straightforward question.
Understanding Factors
Before we delve into the specific factors of 59, let's establish a clear understanding of what a factor is. In mathematics, a factor (or divisor) of a number is a whole number that divides that number exactly, leaving no remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12, because each of these numbers divides 12 without leaving a remainder.
Identifying the Factors of 59
Now, let's turn our attention to the number 59. To find its factors, we need to identify all the whole numbers that divide 59 evenly. We can start by checking the smallest whole numbers:
- 1: 59 divided by 1 is 59, with no remainder. Therefore, 1 is a factor of 59.
- 2: 59 divided by 2 is 29.5, which is not a whole number. Therefore, 2 is not a factor.
- 3: The divisibility rule for 3 states that a number is divisible by 3 if the sum of its digits is divisible by 3. The sum of the digits of 59 (5 + 9 = 14) is not divisible by 3. Therefore, 3 is not a factor.
- 5: A number is divisible by 5 if its last digit is 0 or 5. Since the last digit of 59 is 9, it's not divisible by 5.
- 7: There's no easy divisibility rule for 7, so we perform the division: 59 divided by 7 is approximately 8.43, not a whole number.
- 11: Again, we perform the division: 59 divided by 11 is approximately 5.36, not a whole number.
- 13: 59 divided by 13 is approximately 4.54, not a whole number.
- 17: 59 divided by 17 is approximately 3.47, not a whole number.
- 19: 59 divided by 19 is approximately 3.11, not a whole number.
- 23: 59 divided by 23 is approximately 2.57, not a whole number.
- 29: 59 divided by 29 is approximately 2.03, not a whole number.
- And so on…
As we continue this process, we'll find that the only whole numbers that divide 59 without leaving a remainder are 1 and 59 itself.
59: A Prime Number
This leads us to a crucial conclusion: 59 is a prime number. A prime number is a whole number greater than 1 that has only two factors: 1 and itself. Since the only factors of 59 are 1 and 59, it perfectly fits the definition of a prime number.
Significance of Prime Numbers
Prime numbers are fundamental building blocks in number theory. They are like the "atoms" of numbers, as every other whole number greater than 1 can be expressed as a unique product of prime numbers (this is known as the Fundamental Theorem of Arithmetic). Understanding prime numbers is crucial in cryptography, computer science, and various other fields.
Exploring Divisibility Rules
While we manually checked for divisibility in the case of 59, understanding divisibility rules can significantly speed up the process for other numbers. Here's a brief overview of some common divisibility rules:
- Divisibility by 2: A number is divisible by 2 if its last digit is even (0, 2, 4, 6, or 8).
- Divisibility by 3: A number is divisible by 3 if the sum of its digits is divisible by 3.
- Divisibility by 4: A number is divisible by 4 if the number formed by its last two digits is divisible by 4.
- Divisibility by 5: A number is divisible by 5 if its last digit is 0 or 5.
- Divisibility by 6: A number is divisible by 6 if it is divisible by both 2 and 3.
- Divisibility by 9: A number is divisible by 9 if the sum of its digits is divisible by 9.
- Divisibility by 10: A number is divisible by 10 if its last digit is 0.
These rules can be immensely helpful in quickly determining whether a larger number has certain factors without resorting to long division every time.
Factorization and Prime Factorization
The process of finding the factors of a number is called factorization. When we express a number as a product of its prime factors, it's called prime factorization. For 59, the prime factorization is simply 59, as it's already a prime number.
For composite numbers (numbers that are not prime), prime factorization provides a unique representation. For example, the prime factorization of 12 is 2 x 2 x 3 (or 2² x 3). This unique representation is incredibly useful in various mathematical operations and applications.
Applications of Prime Numbers and Factorization
The concepts of prime numbers and factorization extend far beyond basic arithmetic. They are essential in various fields, including:
-
Cryptography: Modern encryption methods, such as RSA, heavily rely on the difficulty of factoring very large numbers into their prime factors. The security of online transactions and sensitive data often depends on this mathematical principle.
-
Computer Science: Prime numbers play a vital role in algorithm design and data structure optimization. Understanding prime factorization is crucial for efficient data processing and storage.
-
Coding Theory: Error detection and correction codes often use properties of prime numbers to ensure data integrity.
-
Number Theory: Prime numbers are central to many branches of number theory, driving research and discoveries in fundamental mathematics.
Conclusion: The Simplicity and Significance of 59's Factors
The factors of 59, simply 1 and 59, might seem unremarkable at first glance. However, this simplicity highlights the fundamental nature of prime numbers and their importance in mathematics and various other disciplines. Understanding prime factorization and divisibility rules provides a powerful toolset for tackling more complex mathematical problems and exploring the fascinating world of number theory. The seemingly simple question of "What are the factors of 59?" opens a door to a wealth of mathematical concepts with broad and significant applications.
Latest Posts
Latest Posts
-
Which Of The Following Is An Element
Mar 30, 2025
-
Common Multiples Of 12 And 20
Mar 30, 2025
-
Lowest Common Multiple Of 2 And 8
Mar 30, 2025
-
Find The Base Of A Parallelogram
Mar 30, 2025
-
Things That Begin With The Letter N
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about What Is The Factor Of 59 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
