Find The Base Of A Parallelogram
Juapaving
Mar 30, 2025 · 5 min read
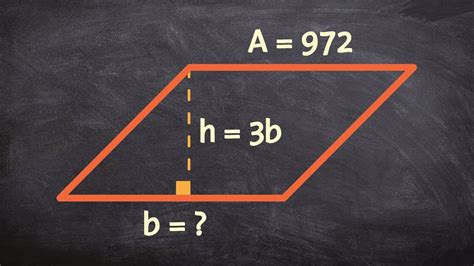
Table of Contents
- Find The Base Of A Parallelogram
- Table of Contents
- Finding the Base of a Parallelogram: A Comprehensive Guide
- Understanding Parallelograms and Their Properties
- Methods for Finding the Base of a Parallelogram
- 1. Using the Area and Height
- 2. Using the Coordinates of the Vertices
- 3. Using Trigonometry and Other Given Angles and Sides
- 4. Using Vector Methods (Advanced)
- 5. Using Similar Triangles (Less Common, but Applicable)
- Practical Applications and Real-World Examples
- Troubleshooting Common Mistakes
- Conclusion
- Latest Posts
- Latest Posts
- Related Post
Finding the Base of a Parallelogram: A Comprehensive Guide
Finding the base of a parallelogram might seem like a straightforward task, but understanding the nuances and different approaches is crucial for solving various geometry problems. This comprehensive guide will delve into the different methods of finding the base, catering to various levels of mathematical understanding, from beginner to advanced. We'll explore various scenarios, including those involving area, height, and other given parameters. This will equip you with the tools to tackle any parallelogram base problem you encounter.
Understanding Parallelograms and Their Properties
Before diving into the methods, let's refresh our understanding of parallelograms. A parallelogram is a quadrilateral (a four-sided polygon) with opposite sides parallel and equal in length. This inherent property is the foundation for all the formulas and techniques we'll use to find the base. Key characteristics include:
- Opposite sides are parallel: This is the defining feature.
- Opposite sides are equal in length: This follows directly from the parallel sides property.
- Opposite angles are equal: Another consequence of the parallel sides.
- Consecutive angles are supplementary: Meaning they add up to 180 degrees.
- Diagonals bisect each other: The diagonals cut each other in half.
Understanding these properties is essential for selecting the appropriate method to determine the base length.
Methods for Finding the Base of a Parallelogram
The method used to find the base depends on the information provided. Here are several common scenarios and their corresponding solutions:
1. Using the Area and Height
This is arguably the most common method. The area of a parallelogram is given by the formula:
Area = base × height
If the area and the height are known, we can easily rearrange the formula to find the base:
base = Area / height
Example: A parallelogram has an area of 60 square centimeters and a height of 10 centimeters. What is the length of its base?
Solution: base = 60 cm² / 10 cm = 6 cm
2. Using the Coordinates of the Vertices
If you know the coordinates of the vertices of the parallelogram on a Cartesian plane, you can use the distance formula to find the length of the base. Let's assume the vertices are A, B, C, and D. The distance formula between two points (x1, y1) and (x2, y2) is:
Distance = √[(x2 - x1)² + (y2 - y1)²]
You'll need to identify which sides are the bases. Remember, opposite sides of a parallelogram are equal in length. Choose any pair of opposite sides; their length will be the base.
Example: A parallelogram has vertices A(1, 2), B(5, 2), C(7, 5), and D(3, 5). Find the length of the base.
Solution: Let's find the distance between A(1, 2) and B(5, 2). Using the distance formula:
Base = √[(5 - 1)² + (2 - 2)²] = √(16 + 0) = 4 units.
Similarly, the distance between C(7, 5) and D(3, 5) is also 4 units, confirming the property of equal opposite sides.
3. Using Trigonometry and Other Given Angles and Sides
If the parallelogram includes angles and sides other than the height and base, trigonometry can be employed. For instance, if you know one side (let's call it 'a') and the angle (θ) between that side and the base, you can use the following trigonometric relationship:
base = a × cos(θ)
Alternatively, if you know the height (h) and the angle (θ) between one side (a) and the height, you can find the base using:
base = a × sin(θ) / sin(α) (where α is the angle between the base and the side a)
Example: A parallelogram has a side of length 8 cm, making an angle of 30 degrees with the base. Find the length of the base.
Solution: base = 8 cm × cos(30°) ≈ 6.93 cm
Important Note: Ensure your calculator is set to degrees and not radians when performing trigonometric calculations.
4. Using Vector Methods (Advanced)
For those familiar with vector algebra, the base of a parallelogram can be determined using vector subtraction and magnitude calculations. If you have the position vectors of the vertices, the difference between the position vectors of two adjacent vertices gives the vector representing one side of the parallelogram. The magnitude of this vector represents the length of that side.
Let's say you have the position vectors of vertices A and B denoted as a and b respectively. Then the vector representing the side AB is given by AB = b - a. The magnitude of this vector (||AB||) gives the length of the side AB. This can represent the base.
5. Using Similar Triangles (Less Common, but Applicable)
In certain geometric problems involving similar triangles within a parallelogram, you might be able to find the base indirectly. This method often involves setting up proportions using the ratios of corresponding sides of similar triangles. This approach requires a detailed understanding of similar triangle properties.
Practical Applications and Real-World Examples
Understanding how to find the base of a parallelogram has numerous practical applications:
- Architecture and Construction: Calculating areas for flooring, roofing, and wall construction.
- Engineering: Determining the dimensions of supporting structures and load-bearing elements.
- Graphic Design and Computer-Aided Design (CAD): Designing layouts and creating geometric shapes.
- Surveying and Land Measurement: Calculating land areas and determining property boundaries.
- Physics: Solving problems related to forces and vectors.
Troubleshooting Common Mistakes
Several common errors can occur when calculating the base of a parallelogram. Be mindful of the following:
- Confusing base and height: Ensure you correctly identify the base and the perpendicular height.
- Incorrect use of trigonometric functions: Double-check that your calculator is in the correct mode (degrees or radians).
- Using the wrong formula: Select the appropriate formula based on the given information.
- Rounding errors: Avoid premature rounding during calculations to minimize errors.
Conclusion
Determining the base of a parallelogram is a fundamental concept in geometry with various applications. While the formula Area = base × height is frequently used, understanding the other methods, including those using coordinates, trigonometry, and vectors, provides a more comprehensive approach to solving diverse geometrical problems. Careful attention to detail, correct formula selection, and awareness of potential errors are crucial for accurate calculations. Remember to always consider the available information and choose the most suitable method. This guide equips you with the knowledge to confidently approach any problem involving parallelogram base calculations.
Latest Posts
Latest Posts
-
What Is The Perimeter Of A Parallelogram
Apr 03, 2025
-
Can A Pure Substance Be Separated By Physical Means
Apr 03, 2025
-
Does A Ribosome Have A Membrane
Apr 03, 2025
-
Is Aluminium A Conductor Of Electricity
Apr 03, 2025
-
A Quadrilateral In Which The Diagonals Bisect Each Other
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Find The Base Of A Parallelogram . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
