What Is The Factor Of 180
Juapaving
Mar 27, 2025 · 6 min read
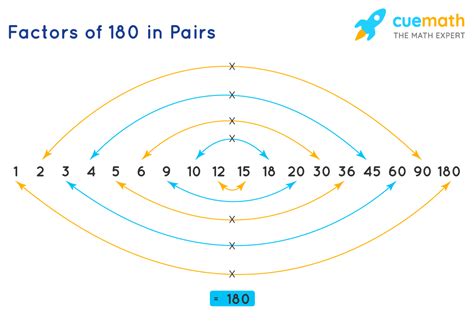
Table of Contents
What are the Factors of 180? A Comprehensive Guide
Finding the factors of a number might seem like a simple mathematical task, but understanding the concept thoroughly unlocks a deeper appreciation of number theory and its applications. This comprehensive guide delves into the factors of 180, exploring different methods to find them, their properties, and their relevance in various mathematical contexts. We'll also touch upon related concepts like prime factorization and the significance of factors in more advanced mathematical problems.
Understanding Factors
Before diving into the factors of 180 specifically, let's define what a factor is. A factor (or divisor) of a number is any integer that divides the number evenly without leaving a remainder. In simpler terms, if you can divide a number by another number without getting a decimal or fraction as a result, the second number is a factor of the first.
For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. Each of these numbers divides 12 without leaving a remainder.
Finding the Factors of 180: Methods and Strategies
There are several ways to find the factors of 180. Let's explore a few:
1. The Pair Method
This method involves systematically finding pairs of numbers that multiply to give 180. We start with 1 and work our way up:
- 1 x 180
- 2 x 90
- 3 x 60
- 4 x 45
- 5 x 36
- 6 x 30
- 9 x 20
- 10 x 18
- 12 x 15
Notice that after 12, we start to repeat pairs (15 x 12 is the same as 12 x 15). This means we've found all the factors.
Therefore, the factors of 180 are: 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90, and 180.
2. Prime Factorization Method
This method uses the prime factorization of the number to find all its factors. Prime factorization involves expressing a number as a product of its prime factors. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself.
Let's find the prime factorization of 180:
180 = 18 x 10 = (2 x 3 x 3) x (2 x 5) = 2² x 3² x 5
Now, to find all the factors, we consider all possible combinations of the prime factors and their exponents:
- 2⁰ x 3⁰ x 5⁰ = 1
- 2¹ x 3⁰ x 5⁰ = 2
- 2² x 3⁰ x 5⁰ = 4
- 2⁰ x 3¹ x 5⁰ = 3
- 2¹ x 3¹ x 5⁰ = 6
- 2² x 3¹ x 5⁰ = 12
- 2⁰ x 3² x 5⁰ = 9
- 2¹ x 3² x 5⁰ = 18
- 2² x 3² x 5⁰ = 36
- 2⁰ x 3⁰ x 5¹ = 5
- 2¹ x 3⁰ x 5¹ = 10
- 2² x 3⁰ x 5¹ = 20
- 2⁰ x 3¹ x 5¹ = 15
- 2¹ x 3¹ x 5¹ = 30
- 2² x 3¹ x 5¹ = 60
- 2⁰ x 3² x 5¹ = 45
- 2¹ x 3² x 5¹ = 90
- 2² x 3² x 5¹ = 180
This method systematically generates all the factors, ensuring none are missed. As you can see, we arrive at the same set of factors as with the pair method.
3. Using a Factor Tree
A factor tree is a visual way to represent the prime factorization of a number. It helps break down the number into its prime components step-by-step.
180
/ \
2 90
/ \
2 45
/ \
3 15
/ \
3 5
From the factor tree, we can read the prime factorization as 2² x 3² x 5, which leads us to the same set of factors as before.
Properties of the Factors of 180
The factors of 180 exhibit several interesting properties:
-
Even and Odd Factors: 180 has both even and odd factors. The even factors are those divisible by 2, while the odd factors are not.
-
Number of Factors: 180 has a total of 18 factors. This can be calculated using the prime factorization. The number of factors is found by adding 1 to each exponent in the prime factorization and then multiplying the results. In this case, (2+1)(2+1)(1+1) = 18.
-
Sum of Factors: The sum of the factors of 180 is 1 + 2 + 3 + 4 + 5 + 6 + 9 + 10 + 12 + 15 + 18 + 20 + 30 + 36 + 45 + 60 + 90 + 180 = 546. This is also known as the sigma function (σ) of 180, denoted as σ(180) = 546.
-
Greatest Common Factor (GCF): The greatest common factor is the largest number that divides two or more numbers without leaving a remainder. For example, the GCF of 180 and 270 is 90.
-
Least Common Multiple (LCM): The least common multiple is the smallest number that is a multiple of two or more numbers. For example, the LCM of 180 and 270 is 540.
Applications of Finding Factors
Understanding factors and prime factorization has broad applications in various mathematical fields, including:
-
Simplifying Fractions: Finding the greatest common factor (GCF) allows you to simplify fractions to their lowest terms.
-
Solving Equations: Factoring expressions is crucial in solving algebraic equations.
-
Number Theory: Factors and prime factorization are fundamental concepts in number theory, used to prove theorems and explore the properties of numbers.
-
Cryptography: Prime numbers and factorization play a vital role in cryptography, securing online communications.
-
Computer Science: Algorithms for factoring large numbers are used in various computer science applications, including cryptography and data security.
Advanced Concepts Related to Factors
-
Perfect Numbers: A perfect number is a positive integer that is equal to the sum of its proper divisors (excluding the number itself). 6 is the smallest perfect number (1 + 2 + 3 = 6). Whether there are infinitely many even perfect numbers remains an unsolved problem in mathematics.
-
Abundant and Deficient Numbers: An abundant number is a number where the sum of its proper divisors is greater than the number itself, while a deficient number is a number where the sum of its proper divisors is less than the number itself. 180 is an abundant number because the sum of its proper divisors (546) is greater than 180.
-
Highly Composite Numbers: A highly composite number is a positive integer with more divisors than any smaller positive integer.
Conclusion: The Significance of Factors
This in-depth exploration of the factors of 180 reveals that seemingly simple mathematical concepts can lead to surprisingly rich and complex mathematical ideas. Understanding how to find factors and their properties is not only essential for basic arithmetic and algebra but also serves as a foundation for more advanced mathematical concepts and their applications across various fields. The ability to efficiently find and manipulate factors is a valuable skill for anyone pursuing a deeper understanding of mathematics and its practical uses. From simplifying fractions to solving complex equations and securing online communications, the power of factorization remains a cornerstone of modern mathematics and computing.
Latest Posts
Latest Posts
-
What Is The Lcm Of 4 5 6
Mar 30, 2025
-
Atomic Number Refers To The Number Of In An Atom
Mar 30, 2025
-
Definition Of Area Model In Math
Mar 30, 2025
-
Matter Is Anything That Has And Occupies
Mar 30, 2025
-
When Ice Cream Melts A Chemical Change Occurs
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about What Is The Factor Of 180 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
