Definition Of Area Model In Math
Juapaving
Mar 30, 2025 · 6 min read
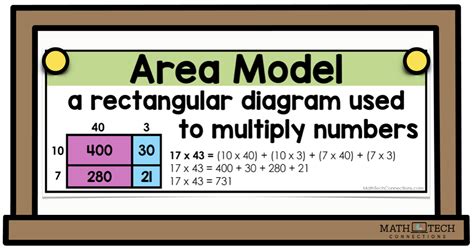
Table of Contents
The Area Model in Math: A Comprehensive Guide
The area model is a powerful visual tool used in mathematics to represent and solve a variety of problems, particularly those involving multiplication, division, and algebraic concepts. Its versatility makes it an invaluable resource for students of all ages, from elementary school through high school and beyond. This comprehensive guide will explore the definition of the area model, delve into its applications across different mathematical contexts, and illustrate its effectiveness with practical examples.
What is the Area Model?
At its core, the area model leverages the geometric concept of area to represent mathematical operations. It's based on the principle that the area of a rectangle is calculated by multiplying its length and width. By visually representing numbers as the dimensions of a rectangle, we can translate multiplication and division into a geometric problem solvable through area calculation. This visual representation makes abstract mathematical concepts more concrete and accessible, particularly for visual learners.
Key Components of the Area Model:
- Rectangles: The foundational element. The dimensions of the rectangle represent the numbers being multiplied or divided.
- Dimensions: The length and width of the rectangle represent the factors in multiplication or the divisor and quotient in division.
- Sub-rectangles: When working with multi-digit numbers, the rectangle is often partitioned into smaller sub-rectangles, each representing partial products.
- Area: The total area of the rectangle represents the product in multiplication or the dividend in division.
Applications of the Area Model:
The area model's flexibility extends its use across numerous mathematical concepts. Let's explore some key applications:
1. Multiplication of Whole Numbers:
The area model excels in illustrating the distributive property of multiplication. Consider multiplying 23 by 14:
-
Step 1: Represent the numbers: Draw a rectangle. Label one side as 20 + 3 (representing 23) and the other side as 10 + 4 (representing 14).
-
Step 2: Partition the rectangle: Divide the rectangle into four smaller sub-rectangles based on the decomposed numbers.
-
Step 3: Calculate the area of each sub-rectangle: Each sub-rectangle's area represents a partial product:
- 20 x 10 = 200
- 20 x 4 = 80
- 3 x 10 = 30
- 3 x 4 = 12
-
Step 4: Sum the partial products: Add the areas of all sub-rectangles: 200 + 80 + 30 + 12 = 322. Therefore, 23 x 14 = 322.
This method clarifies how each digit contributes to the final product, providing a deeper understanding than traditional algorithms.
2. Multiplication of Decimals:
The area model seamlessly adapts to decimal multiplication. The process remains the same, but now the dimensions represent decimal numbers. Consider 1.2 x 3.5:
-
Step 1: Represent the numbers: Draw a rectangle. Label one side as 1 + 0.2 and the other as 3 + 0.5.
-
Step 2: Partition the rectangle: Divide the rectangle into four sub-rectangles.
-
Step 3: Calculate the area of each sub-rectangle:
- 1 x 3 = 3
- 1 x 0.5 = 0.5
- 0.2 x 3 = 0.6
- 0.2 x 0.5 = 0.1
-
Step 4: Sum the partial products: 3 + 0.5 + 0.6 + 0.1 = 4.2. Therefore, 1.2 x 3.5 = 4.2.
This approach makes understanding decimal place values and their impact on the final product more intuitive.
3. Multiplication of Fractions:
The area model is incredibly effective for visualizing fraction multiplication. Consider multiplying 2/3 x 3/4:
-
Step 1: Represent the fractions: Draw a rectangle. Let the whole rectangle represent "1".
-
Step 2: Divide the rectangle: Divide the rectangle into four equal parts horizontally (representing the denominator of 3/4). Shade 3 of these parts to visually represent 3/4.
-
Step 3: Further divide: Divide the rectangle into three equal parts vertically (representing the denominator of 2/3).
-
Step 4: Identify the overlapping area: The overlapping area of the shaded parts represents the product. Count the overlapping squares and divide by the total number of squares. There are 6 overlapping squares out of 12 total squares, which simplifies to 6/12 = 1/2. Therefore, 2/3 x 3/4 = 1/2.
This visual representation makes understanding the multiplication of fractions significantly easier, clarifying the concept of finding a fraction of a fraction.
4. Division of Whole Numbers:
The area model can also be adapted for division. Imagine dividing 48 by 6:
-
Step 1: Represent the dividend: Draw a rectangle with an area of 48.
-
Step 2: Represent the divisor: You know one side of the rectangle is 6 (the divisor).
-
Step 3: Determine the other side: To find the other side (the quotient), determine what number multiplied by 6 equals 48. You can use trial and error, or break down 48 into factors that include 6 (6 x 8 = 48).
-
Step 4: The quotient: The length of the unknown side represents the quotient. In this case, the other side is 8, so 48 ÷ 6 = 8.
This approach allows for a visual understanding of the relationship between the dividend, divisor, and quotient.
5. Algebra and Polynomials:
The area model extends its power to more advanced mathematics. It can be used to multiply binomials, expanding expressions like (x + 2)(x + 3):
-
Step 1: Represent the binomials: Draw a rectangle. Label the sides as (x + 2) and (x + 3).
-
Step 2: Partition the rectangle: Divide the rectangle into four sub-rectangles.
-
Step 3: Calculate the area of each sub-rectangle:
- x * x = x²
- x * 3 = 3x
- 2 * x = 2x
- 2 * 3 = 6
-
Step 4: Combine like terms: The total area is x² + 3x + 2x + 6 = x² + 5x + 6. Thus, (x + 2)(x + 3) = x² + 5x + 6.
Advantages of Using the Area Model:
- Visual Representation: Makes abstract concepts more concrete and easier to grasp.
- Improved Understanding: Provides a deeper understanding of the underlying mathematical principles.
- Versatility: Applicable across various mathematical operations and concepts.
- Problem-Solving Skills: Enhances problem-solving skills by providing a visual framework.
- Engaging and Interactive: Creates a more engaging learning experience.
Comparing the Area Model to Traditional Algorithms:
While traditional algorithms are efficient for quick calculations, the area model offers significant advantages in understanding why the algorithms work. It provides a visual context that traditional methods often lack. This deeper understanding is crucial for building a strong foundation in mathematics.
Conclusion:
The area model is a versatile and effective tool that significantly enhances mathematical understanding. Its visual nature makes complex concepts accessible, improving comprehension and fostering a deeper appreciation for the underlying principles. From elementary multiplication to advanced algebraic manipulations, the area model proves its worth as an invaluable teaching and learning resource, empowering students to confidently tackle various mathematical challenges. Its adaptability and clarity make it a fundamental tool in the mathematical toolkit. By leveraging the power of visual representation, the area model transforms abstract mathematical concepts into tangible, easily understood geometric problems.
Latest Posts
Latest Posts
-
What Is The Lcm Of 26 And 39
Apr 01, 2025
-
What Are The Common Factors Of 56
Apr 01, 2025
-
Which Noble Gas Has The Highest First Ionization Energy
Apr 01, 2025
-
1000 Meters Is Equal To How Many Kilometers
Apr 01, 2025
-
The Type Of Life Cycle Seen In Plants Is Called
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Definition Of Area Model In Math . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
