What Is The Area Of Triangle Abc
Juapaving
Mar 25, 2025 · 5 min read
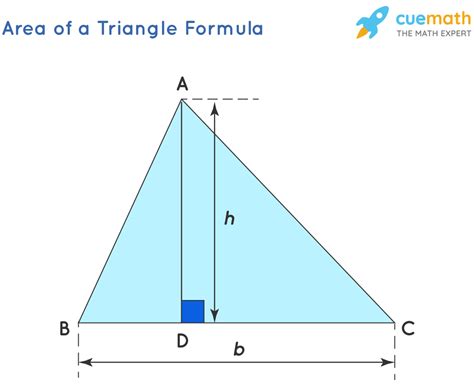
Table of Contents
What is the Area of Triangle ABC? A Comprehensive Guide
Determining the area of a triangle is a fundamental concept in geometry with widespread applications in various fields, from surveying and architecture to computer graphics and physics. While the formula for the area of a triangle, ½ * base * height, is commonly known, understanding its derivation and the various methods for calculating the area, particularly when dealing with triangles lacking a readily available height, is crucial. This comprehensive guide delves into the different approaches to finding the area of triangle ABC, explaining the underlying principles and providing practical examples.
Understanding the Basic Formula: ½ * base * height
The most straightforward method to find the area of any triangle is using the formula: Area = ½ * base * height. This formula works because a triangle can be viewed as half of a parallelogram. The parallelogram has the same base and height as the triangle, and its area is base * height. Consequently, the triangle's area is exactly half of that.
Key Considerations:
- Base: Any side of the triangle can be chosen as the base.
- Height: The height is the perpendicular distance from the vertex opposite the chosen base to the base itself (or its extension). It's crucial that the height is perpendicular; otherwise, the formula will not yield the correct result.
Example:
Let's consider a triangle ABC with base AB = 6 units and height h = 4 units.
Area = ½ * 6 * 4 = 12 square units
Beyond the Basic: Alternative Methods for Calculating Area
While the ½ * base * height formula is fundamental, it's not always the most practical approach. When the height isn't readily available or easily calculable, other methods become necessary. These include:
1. Heron's Formula
Heron's formula is exceptionally useful when you know the lengths of all three sides of the triangle but not the height. This is particularly beneficial when dealing with triangles that aren't right-angled.
Formula:
Area = √[s(s-a)(s-b)(s-c)]
Where:
- a, b, and c are the lengths of the sides of the triangle.
- s is the semi-perimeter, calculated as s = (a + b + c) / 2
Example:
Consider a triangle with sides a = 5, b = 6, and c = 7.
- Calculate the semi-perimeter: s = (5 + 6 + 7) / 2 = 9
- Apply Heron's formula: Area = √[9(9-5)(9-6)(9-7)] = √[9 * 4 * 3 * 2] = √216 ≈ 14.7 square units
2. Using Trigonometry: Area = ½ * a * b * sin(C)
This method uses trigonometry to calculate the area when you know the lengths of two sides and the angle between them.
Formula:
Area = ½ * a * b * sin(C)
Where:
- a and b are the lengths of two sides of the triangle.
- C is the angle between sides a and b.
Example:
Let's say we have a triangle with sides a = 8, b = 10, and the angle C between them is 30 degrees.
Area = ½ * 8 * 10 * sin(30°) = 40 * 0.5 = 20 square units
3. Coordinate Geometry Approach
If the vertices of the triangle are given as coordinates in a Cartesian plane (x, y), the area can be calculated using the determinant method.
Formula:
Area = 0.5 * |(x₁ (y₂ - y₃) + x₂ (y₃ - y₁) + x₃ (y₁ - y₂))|
Where:
- (x₁, y₁), (x₂, y₂), and (x₃, y₃) are the coordinates of the vertices A, B, and C, respectively.
- The vertical bars | | denote the absolute value.
Example:
Let's consider a triangle with vertices A(1, 1), B(4, 2), and C(2, 5).
Area = 0.5 * |(1(2 - 5) + 4(5 - 1) + 2(1 - 2))| = 0.5 * |(-3 + 16 - 2)| = 0.5 * 11 = 5.5 square units
Choosing the Right Method: A Practical Guide
The best method for calculating the area of triangle ABC depends on the information available:
- If you know the base and height: Use the ½ * base * height formula. This is the simplest and most direct method.
- If you know all three side lengths: Use Heron's formula. This is particularly useful for non-right-angled triangles.
- If you know two sides and the included angle: Use the trigonometric formula (½ * a * b * sin(C)). This method is efficient when dealing with angles.
- If you know the coordinates of the vertices: Use the coordinate geometry approach. This is useful when dealing with triangles represented on a coordinate plane.
Applications of Triangle Area Calculation
The ability to calculate the area of a triangle has numerous applications across various disciplines:
- Surveying and Land Measurement: Determining the area of land parcels often involves breaking down irregular shapes into triangles.
- Architecture and Engineering: Calculating the area of triangular sections in buildings and structures is crucial for design and material estimations.
- Computer Graphics: Triangles are fundamental building blocks in computer graphics, used to render complex 3D models. Calculating their areas is essential for shading, texturing, and other graphical processes.
- Physics: Triangle areas are used in various physics calculations, including those related to forces, vectors, and areas under curves.
Advanced Concepts and Further Exploration
For those interested in delving deeper, exploring these advanced concepts will enhance your understanding of triangle area calculations:
- Area of a triangle using vectors: The area of a triangle can also be calculated using the cross product of two vectors representing two sides of the triangle.
- Triangle inequality theorem: This theorem states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side. Understanding this theorem helps in validating the dimensions of a triangle before applying any area calculation method.
- Relationship between area and circumradius/inradius: The area of a triangle is related to both its circumradius (the radius of the circumscribed circle) and inradius (the radius of the inscribed circle) through specific formulas.
Conclusion
Calculating the area of triangle ABC is a multifaceted problem with several solution paths. Mastering these different methods empowers you to tackle a variety of geometric problems effectively. Understanding the underlying principles and choosing the appropriate method based on the available data is crucial for achieving accurate results. Remember to always double-check your calculations and consider the context of the problem to select the most efficient and appropriate approach. The ability to efficiently and accurately calculate the area of a triangle is a valuable skill with diverse real-world applications.
Latest Posts
Latest Posts
-
What Is The Least Common Multiple Of 18 And 6
Mar 27, 2025
-
Which State Of Matter Has A Definite Shape And Volume
Mar 27, 2025
-
What Is The S I Unit For Temperature
Mar 27, 2025
-
Write A Short Note On Apiculture
Mar 27, 2025
-
Dissolving Sugar In Water Is A Chemical Change
Mar 27, 2025
Related Post
Thank you for visiting our website which covers about What Is The Area Of Triangle Abc . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
