What Is All The Factors Of 39
Juapaving
Mar 29, 2025 · 6 min read
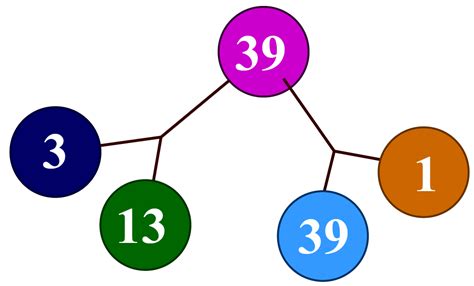
Table of Contents
What are all the factors of 39? A Deep Dive into Prime Factorization and Divisibility
Finding all the factors of a number might seem like a simple mathematical task, but it's a fundamental concept with far-reaching applications in number theory, cryptography, and even computer science. This article will explore the factors of 39, delving into the methods for identifying them, understanding their significance, and connecting this seemingly basic concept to broader mathematical principles. We'll cover prime factorization, divisibility rules, and explore the unique properties of factors, particularly within the context of the number 39.
Understanding Factors and Divisibility
Before we dive into the factors of 39, let's solidify our understanding of fundamental terms. A factor (or divisor) of a number is any integer that divides the number without leaving a remainder. In simpler terms, it's a number that can be multiplied by another whole number to produce the original number. Divisibility is the property of one number being exactly divisible by another.
For example, the number 12 is divisible by 2, 3, 4, and 6 because each of these numbers divides 12 without leaving a remainder. Therefore, 1, 2, 3, 4, 6, and 12 are all factors of 12.
Finding the Factors of 39: A Step-by-Step Approach
Now, let's determine all the factors of 39. The most straightforward method is to systematically test each integer starting from 1 to see if it divides 39 without a remainder.
- Start with 1: 39 divided by 1 is 39, so 1 is a factor.
- Check for 2: 39 is not divisible by 2 (it's an odd number).
- Check for 3: 39 divided by 3 is 13, so 3 is a factor.
- Check for 4: 39 is not divisible by 4.
- Check for 5: 39 is not divisible by 5.
- Check for 6: 39 is not divisible by 6.
- Check for 7: 39 is not divisible by 7.
- Check for 8: 39 is not divisible by 8.
- Check for 9: 39 is not divisible by 9.
- Check for 10: 39 is not divisible by 10.
- Check for 11: 39 is not divisible by 11.
- Check for 12: 39 is not divisible by 12.
- Check for 13: 39 divided by 13 is 3, so 13 is a factor.
Notice that we've reached 13. Since 13 multiplied by 3 equals 39, and 13 is greater than the square root of 39 (approximately 6.24), we've found all the factors. Any factors beyond 13 would have a corresponding factor less than 3, and we've already checked those.
Therefore, the factors of 39 are 1, 3, 13, and 39.
Prime Factorization: Unveiling the Building Blocks
A more elegant and powerful method for finding factors is prime factorization. This involves breaking down a number into its prime factors – prime numbers that when multiplied together give the original number. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself.
The prime factorization of 39 is 3 x 13. Both 3 and 13 are prime numbers. This prime factorization helps us understand the fundamental building blocks of 39 and quickly identify all its factors.
How Prime Factorization Helps Find All Factors
Once you have the prime factorization, finding all factors becomes relatively straightforward. You systematically combine the prime factors in different ways. In the case of 39 (3 x 13):
- 1: The product of no prime factors (or the empty product, which equals 1).
- 3: The product of just the prime factor 3.
- 13: The product of just the prime factor 13.
- 39: The product of both prime factors, 3 and 13.
This method ensures we find all factors without missing any.
Divisibility Rules: Shortcuts and Efficiency
Divisibility rules provide helpful shortcuts to quickly determine if a number is divisible by certain integers without performing the full division. Knowing these rules can significantly speed up the process of finding factors. Some relevant divisibility rules include:
- Divisibility by 2: A number is divisible by 2 if it is an even number (ends in 0, 2, 4, 6, or 8).
- Divisibility by 3: A number is divisible by 3 if the sum of its digits is divisible by 3. (3 + 9 = 12, which is divisible by 3, so 39 is divisible by 3).
- Divisibility by 5: A number is divisible by 5 if it ends in 0 or 5.
- Divisibility by 10: A number is divisible by 10 if it ends in 0.
Applying these rules allows for efficient preliminary checks before performing division, saving time and effort, particularly when dealing with larger numbers.
The Significance of Factors in Mathematics and Beyond
The concept of factors extends far beyond simple division problems. It plays a crucial role in various areas of mathematics and its applications:
- Number Theory: Factors are central to understanding concepts like prime numbers, greatest common divisors (GCD), and least common multiples (LCM). These concepts are foundational to many areas of advanced mathematics.
- Cryptography: Prime factorization forms the basis of many modern cryptographic systems, including RSA encryption. The difficulty of factoring very large numbers into their prime components is what makes these systems secure.
- Computer Science: Algorithms for finding factors and prime factorizations are used in various computational tasks, from optimizing code to analyzing data structures.
- Algebra: Factors are crucial in simplifying algebraic expressions and solving equations.
Exploring the Properties of the Factors of 39
Let's examine some interesting properties of the factors of 39:
- Pairwise Relationship: The factors of 39 (1, 3, 13, 39) show a pairwise relationship. 1 x 39 = 39 and 3 x 13 = 39. This is a common property of factors; they often come in pairs whose product equals the original number.
- Sum of Factors: The sum of the factors of 39 (1 + 3 + 13 + 39) is 56. The sum of factors has applications in number theory, particularly in the study of perfect numbers and abundant numbers.
- Relationship to Prime Factorization: The number of factors can be easily determined from the prime factorization. If the prime factorization is p<sup>a</sup> x q<sup>b</sup> x r<sup>c</sup>..., the number of factors is (a+1)(b+1)(c+1)... For 39 (3<sup>1</sup> x 13<sup>1</sup>), the number of factors is (1+1)(1+1) = 4, which is exactly the number of factors we found.
Conclusion: Factors of 39 and the Broader Picture
Finding the factors of 39, while a seemingly elementary task, provides a valuable entry point into the fascinating world of number theory and its applications. By understanding the methods for identifying factors, utilizing prime factorization, and appreciating the significance of divisibility rules, we gain a deeper understanding of mathematical concepts that underpin many advanced fields. The simple number 39, therefore, becomes a gateway to exploring a complex and rich mathematical landscape. Remember, the seemingly mundane can often lead to the extraordinary when we approach it with curiosity and a desire to understand.
Latest Posts
Latest Posts
-
70 As A Product Of Prime Factors
Mar 31, 2025
-
A Ray Has Two Endpoints True Or False
Mar 31, 2025
-
A Substance That Cannot Be Broken Down By Chemical Means
Mar 31, 2025
-
Do Both Prokaryotic And Eukaryotic Cells Have Ribosomes
Mar 31, 2025
-
Which Law Represents A Balanced Chemical Equation
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is All The Factors Of 39 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
