What Is A Subset Of A Real Number
Juapaving
Mar 28, 2025 · 5 min read
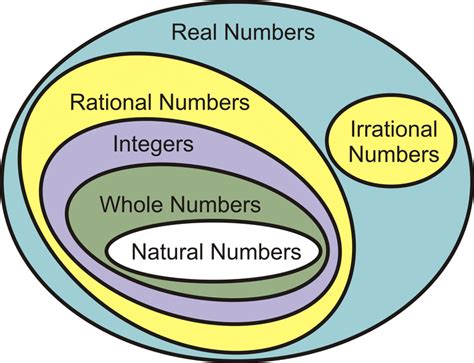
Table of Contents
What is a Subset of a Real Number? A Comprehensive Guide
The real numbers, denoted by ℝ, form the foundation of much of mathematics. Understanding their subsets is crucial for grasping more advanced concepts in calculus, analysis, linear algebra, and many other fields. This comprehensive guide will delve deep into the subsets of real numbers, exploring their definitions, properties, and significance. We’ll cover everything from the basics to more nuanced topics, ensuring a thorough understanding for readers of all levels.
Understanding the Real Number System
Before diving into subsets, let's refresh our understanding of the real number system itself. The real numbers encompass all rational and irrational numbers.
Rational Numbers (ℚ)
Rational numbers are numbers that can be expressed as a fraction p/q, where p and q are integers, and q is not zero. Examples include:
- Integers (ℤ): Whole numbers, including positive integers (1, 2, 3...), negative integers (-1, -2, -3...), and zero (0). Integers are a subset of rational numbers since they can be written as p/1.
- Fractions: Numbers like 1/2, 3/4, -2/5, etc.
Irrational Numbers
Irrational numbers cannot be expressed as a fraction of two integers. They have decimal representations that neither terminate nor repeat. Famous examples include:
- π (Pi): The ratio of a circle's circumference to its diameter, approximately 3.14159...
- e (Euler's number): The base of the natural logarithm, approximately 2.71828...
- √2 (Square root of 2): This number cannot be expressed as a fraction.
The union of rational and irrational numbers constitutes the complete set of real numbers (ℝ).
Key Subsets of Real Numbers
Now, let's explore some important subsets within the real number system. Understanding these subsets is essential for comprehending many mathematical concepts.
1. Natural Numbers (ℕ)
Natural numbers are the positive integers: {1, 2, 3, 4, ...}. They are often used in counting and enumeration. They form the foundation for many mathematical structures. It's important to note that the inclusion of 0 in the natural numbers is a matter of convention; some definitions include 0, while others do not.
Properties of Natural Numbers:
- Closure under addition and multiplication: Adding or multiplying two natural numbers always results in another natural number.
- Well-ordering principle: Every non-empty subset of natural numbers has a least element. This property is fundamental in many proofs.
2. Integers (ℤ)
As mentioned earlier, integers include all whole numbers, both positive and negative, and zero: {..., -3, -2, -1, 0, 1, 2, 3, ...}. They extend the natural numbers to include negative counterparts.
Properties of Integers:
- Closure under addition, subtraction, and multiplication: Performing these operations on integers always yields another integer.
- Additive inverses: Every integer has an additive inverse (its negative).
3. Rational Numbers (ℚ)
Rational numbers, as discussed above, can be expressed as fractions p/q, where p and q are integers, and q ≠ 0.
Properties of Rational Numbers:
- Dense: Between any two distinct rational numbers, there exists another rational number. This implies that rational numbers are densely packed on the number line.
- Countable: While dense, the rational numbers are countable, meaning they can be put into a one-to-one correspondence with the natural numbers.
4. Irrational Numbers (ℝ \ ℚ)
Irrational numbers are real numbers that are not rational. Their decimal representations are non-terminating and non-repeating.
Properties of Irrational Numbers:
- Uncountable: Unlike rational numbers, irrational numbers are uncountable, meaning they cannot be put into a one-to-one correspondence with the natural numbers.
- Examples: π, e, √2, √3, etc.
5. Real Numbers (ℝ)
The real numbers encompass all rational and irrational numbers. They can be visualized as points on a number line, extending infinitely in both positive and negative directions.
Properties of Real Numbers:
- Completeness: The real numbers satisfy the completeness axiom, which essentially states that every non-empty set of real numbers that is bounded above has a least upper bound (supremum). This is a crucial property in analysis.
- Uncountable: The real numbers are uncountable, a consequence of the uncountability of irrational numbers.
6. Intervals
Intervals are subsets of real numbers defined by their endpoints. They can be open, closed, or half-open.
- Open Interval: (a, b) = {x ∈ ℝ | a < x < b} The endpoints are not included.
- Closed Interval: [a, b] = {x ∈ ℝ | a ≤ x ≤ b} The endpoints are included.
- Half-Open Intervals: [a, b) = {x ∈ ℝ | a ≤ x < b} and (a, b] = {x ∈ ℝ | a < x ≤ b}
7. Bounded and Unbounded Sets
- Bounded Set: A set of real numbers is bounded if it has both an upper bound (a number greater than or equal to all elements) and a lower bound (a number less than or equal to all elements).
- Unbounded Set: A set that is not bounded. For example, the set of all real numbers is unbounded.
8. Open and Closed Sets
These concepts are more advanced and crucial in topology and analysis.
- Open Set: A set S is open if for every point x in S, there exists an open interval containing x that is entirely contained within S.
- Closed Set: A set S is closed if its complement (the set of all real numbers not in S) is open.
Significance of Subsets in Mathematics
The various subsets of real numbers play critical roles in different areas of mathematics:
- Calculus: Understanding intervals is fundamental for defining limits, derivatives, and integrals. The concept of completeness is crucial for proving many theorems in calculus.
- Real Analysis: This field heavily relies on the properties of real numbers and their subsets, particularly concerning convergence, continuity, and differentiability.
- Linear Algebra: Real numbers form the scalars in vector spaces, and understanding their subsets is crucial for working with vectors and matrices.
- Topology: Open and closed sets are fundamental concepts in topology, a field that studies the properties of spaces that are preserved under continuous deformations.
- Probability and Statistics: Real numbers are used to represent probabilities and statistical measures, and understanding intervals and bounded sets is essential in these fields.
Conclusion
The real number system and its subsets form the bedrock of much of mathematics. A solid grasp of these concepts – from natural numbers to open and closed sets – is essential for anyone pursuing advanced mathematical studies. This guide has provided a comprehensive overview, touching upon key definitions, properties, and their importance across various branches of mathematics. Continued exploration and practice will solidify your understanding and pave the way for tackling more complex mathematical concepts. Remember to continuously review and apply this knowledge to reinforce your understanding of this fundamental topic.
Latest Posts
Latest Posts
-
Mass Of An Electron In Mev
Mar 31, 2025
-
From A Gas To A Liquid
Mar 31, 2025
-
How Many Feet Is 16 Meters
Mar 31, 2025
-
Examples Of Gas To A Liquid
Mar 31, 2025
-
Horizontal Cross Section Of A Cone
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is A Subset Of A Real Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
