What Is A Adjacent Supplementary Angle
Juapaving
Mar 30, 2025 · 6 min read
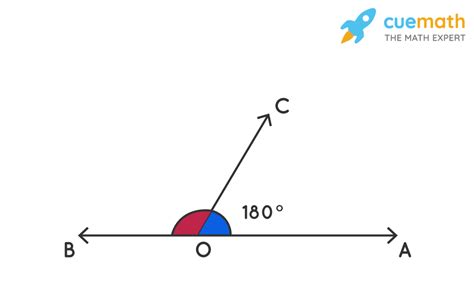
Table of Contents
What is an Adjacent Supplementary Angle? A Deep Dive into Geometry
Understanding angles is fundamental to geometry and numerous applications in various fields, from architecture and engineering to computer graphics and game development. Among the different types of angles, adjacent supplementary angles hold a unique position. This comprehensive guide will explore the definition, properties, examples, and real-world applications of adjacent supplementary angles, ensuring a thorough understanding of this crucial geometric concept.
Defining Adjacent Supplementary Angles
Before delving into the specifics of adjacent supplementary angles, let's first clarify the individual terms:
Supplementary Angles: Two angles are considered supplementary if their sum equals 180 degrees (or π radians). They don't necessarily need to be adjacent; they simply need to add up to the straight angle.
Adjacent Angles: Adjacent angles share a common vertex (the point where the two rays meet) and a common side. They are "next to" each other, but they don't overlap.
Bringing it Together: Adjacent Supplementary Angles
Therefore, adjacent supplementary angles are two angles that are both adjacent (share a common vertex and side) and supplementary (add up to 180 degrees). They form a linear pair – meaning they lie on a straight line. This is a key characteristic; if angles are adjacent and supplementary, they automatically form a linear pair. Conversely, if angles form a linear pair, they are necessarily adjacent and supplementary.
Think of it like this: imagine a straight line. Now, draw a ray from any point on the line. The two angles created on either side of that ray are adjacent supplementary angles. Their sum must always be 180 degrees.
Properties of Adjacent Supplementary Angles
Several key properties define adjacent supplementary angles:
-
Sum equals 180°: The most fundamental property is that the sum of their measures is always 180 degrees. This is the defining characteristic of supplementary angles.
-
Adjacent: They share a common vertex and a common side. They are positioned next to each other, without any overlap.
-
Linear Pair: As mentioned earlier, they always form a linear pair. This means they are adjacent and their non-common sides form a straight line.
-
One Angle Determines the Other: Knowing the measure of one adjacent supplementary angle automatically reveals the measure of the other. If one angle is x degrees, the other will be (180 - x) degrees.
Identifying Adjacent Supplementary Angles: Examples and Illustrations
Let's look at some examples to solidify the concept:
Example 1:
Imagine two angles, ∠A and ∠B. ∠A measures 110 degrees, and ∠B measures 70 degrees. Are they adjacent supplementary angles?
They are supplementary (110° + 70° = 180°), but we need more information to determine if they are adjacent. If they share a common vertex and a common side, then yes, they are adjacent supplementary angles. If not, they are only supplementary.
Example 2:
Consider two angles, ∠C and ∠D, formed by intersecting lines. These angles are vertically opposite. Are they adjacent supplementary angles?
Vertically opposite angles are equal, but they do not share a common side, thus they are not adjacent and therefore not adjacent supplementary angles. They are merely supplementary if the sum of their measurements is 180 degrees.
Example 3:
Two angles, ∠E and ∠F, form a straight line. ∠E is 45°. What is the measure of ∠F?
Since they form a straight line, they are adjacent supplementary angles. Therefore, ∠F = 180° - 45° = 135°.
Example 4 (Visual):
Imagine a square. Each corner of the square represents four adjacent supplementary angles. Each of these angles is a right angle (90°), and two right angles next to each other (adjacent angles) add up to 180°.
Adjacent Supplementary Angles in Real-World Applications
The concept of adjacent supplementary angles isn't just a theoretical exercise; it has numerous practical applications:
-
Architecture and Construction: Understanding adjacent supplementary angles is crucial for architects and construction workers. They need to ensure that angles in structures, such as walls, roofs, and beams, meet the required specifications. Incorrect angles can lead to structural instability.
-
Engineering: Engineers rely on precise angles in designing bridges, roads, and other infrastructure projects. Adjacent supplementary angles ensure that components fit together correctly and the structure is stable and functional.
-
Computer Graphics and Game Development: In creating realistic 3D models and environments, accurate angle calculations are essential. Adjacent supplementary angles are frequently used in determining the positions and orientations of objects and lighting sources.
-
Navigation: Accurate navigation often relies on understanding angles and directions. Determining the correct course requires considering the relationships between different angles, which may include adjacent supplementary angles.
-
Cartography: Creating accurate maps relies on precise measurements of angles and distances. Understanding the relationship between different angles, including adjacent supplementary angles, plays a vital role in map creation.
-
Surveying: Land surveying involves measuring angles to determine boundaries and elevations. Using the principles of adjacent supplementary angles ensures the accuracy of survey measurements.
Differentiating Adjacent Supplementary Angles from Other Angle Relationships
It's important to distinguish adjacent supplementary angles from other angle relationships:
-
Supplementary Angles (Non-Adjacent): Two angles that sum to 180° but don't share a common side or vertex.
-
Complementary Angles: Two angles that sum to 90°.
-
Vertical Angles: Angles opposite each other when two lines intersect. They are always equal but not necessarily adjacent.
-
Adjacent Angles (Non-Supplementary): Two angles that share a common vertex and side but don't add up to 180°.
Solving Problems Involving Adjacent Supplementary Angles
Many geometry problems involve finding the measure of an unknown angle when given the measure of its adjacent supplementary angle. Here's a step-by-step approach:
-
Identify the Adjacent Supplementary Angles: Clearly identify the two angles that are adjacent and share a common side.
-
Set up an Equation: Knowing that their sum is 180°, create an equation representing this relationship. If one angle is 'x', the other will be '180 - x'.
-
Solve for the Unknown: Solve the equation for the unknown variable (x).
-
Check Your Answer: Substitute your solution back into the equation to verify that the sum is indeed 180°.
Conclusion: The Significance of Adjacent Supplementary Angles
Adjacent supplementary angles are a fundamental concept in geometry with far-reaching applications. Understanding their definition, properties, and real-world implications is crucial for anyone studying mathematics, engineering, design, or any field involving spatial reasoning. By mastering this concept, you gain a deeper appreciation for the intricate relationships between angles and their significance in shaping our world. From the architecture of buildings to the intricate workings of computer-generated imagery, the principles governing adjacent supplementary angles remain constant and irreplaceable. Their consistent presence in diverse fields highlights their fundamental importance in understanding and interpreting the world around us.
Latest Posts
Latest Posts
-
Relationship Between Degree Celsius And Fahrenheit
Apr 01, 2025
-
What Is The Lcm Of 26 And 39
Apr 01, 2025
-
What Are The Common Factors Of 56
Apr 01, 2025
-
Which Noble Gas Has The Highest First Ionization Energy
Apr 01, 2025
-
1000 Meters Is Equal To How Many Kilometers
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Is A Adjacent Supplementary Angle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
